連立方程式(代入法1) 連立方程式を解け x=4y5 x7y=11 y=2x1 5xy=4 x4y=13 x=3y1 7xy=17 y=5x13 x=2y14 x3y=27 y=2x10 3xy=18 2x5y=6 x=4y9 2x3y=2 y=3x25 x=4y10 7x3y=39 y=2x17 3x4y=134x5y=31 x=3y13 12x5y=21 y=2x13 例題 代入法①1 次の連立方程式を代入法で解きなさい。(1) \(\begin{cases}x2y=7&\cdots①\\ x=3y8&\cdots②\end{cases}\)(2) \(\begin{cases}3xy=1&\cdots①\\ y=x1&\cdots②\end{cases}\)例題 代入法②1 次の連立方程式を代入法で解きなさい 単元 連立方程式, 「対象\b:中1 中2 中3 ⭐️⭐️⭐️やる気スイッチを、入れませんか?⭐️⭐️⭐️ 個別指導学習塾スクールIEはこんな学習塾です。 ・まずは独自の診断ツールであなたの性格と学力を分析します ・診断結果に基づいてあなたに合った講師を選びます ・世界に一冊
連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
連立方程式 代入法 例題
連立方程式 代入法 例題- 連立方程式の解き方基本:加減法 加減法とは、わかりやすくいえば ステップ1:複数の方程式が共通して持つ文字の中から1つの文字を選び、その文字の係数をそろえる ステップ2:係数をそろえた文字が消去できるように、方程式を足したり引いたりするX62 直接法と反復法 連立1次方程式の解法は直接法と反復法に分類される. 第5章の例題31 で得られた連立1次方程式 0 b b b @ 4 1 1 0 1 2 0 1=2 1 0 2 1=2 0 1=2 =2 1 1 c c c a 0 b b b @ u1 u2 u3 u4 1 c c c a = 0 b b b @ 1=4 1=8 1=8 1=12 1 c c c a 後退代入 第4行の方程式




連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト
例題12 家から学校まで 10 mあります.途中の橋まで毎分 50 mの速さで歩き,橋から学校まで毎分 80 mの速さで歩いたら,合計で 15 分かかりました.家から橋まで,橋から学校までそれぞれ何分歩きましたか. (1) 家から橋まで x 分,橋から学校まで y 分歩い[例題 A] 次の連立方程式を解きなさい. y=2x1(1) y=3x−5(2) この形の連立方程式は,(1)の右辺を(2)の yのところに「代入」して, yを消去すれば解けます.連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく
連立方程式(代入法2) 連立方程式を解け 3x=4y11 3x7y=17 2y=3x4 5x2y=8 2x5y=16 2x=7yx3y=1 3y=4x7 4x=5y10 4x7y=22 5y=2x16 3x5y=92x5y=23 2x=3y1 2x7y=5 7y=3x4 8x=5y98x3y=31 6y=5x157x6y=334x5y=23 4x=3y17 12x5y=27 5y=9x9 連立方程式の代入法の解き方 を解説していくよ。 よかったら参考にしてみてね^^ 連立方程式の代入法の解き方がわかる4つのステップ 例題といっしょに解説していくよ。 例題 つぎの連立方程式を代入法で解きなさい。 2x 3y = 14 3x y = 0 代入法はつぎの42つの文字 が含まれている連立方程式を解くには,加減法や代入法を使って,どちらか一方の文字を消去し,1つの文字だけの方程式に直して解くようにします. この問題のように の形の式があると ,代入によって を消去することができます. 解き方の
となりこの連立方程式を解くことが出来ました! ②代入法 続いて代入法について説明します! 代入法は片方の式をもう一方に代入して文字を減らす方法です。 こちらも先ほどの例題で解説していきます! Cプログラミング ー連立1次方程式の解法一 早稲田大学 本日の目標 連立一次方程式の解法 ガウスの消去法 前進消去 後退代入 NaN・INFINITY ・部分ピホット選択付きカウスの消去法 連立1次方程式の解法 逆行列を用いる方法 クラメール(Cremer)の公式 直接連立方程式を代入法で解く ことができる。 提示用教材③④ 代入法による連立方程式の解き方 代入法で連立方程式を解 くことができる。 提示用教材③ かっこをふくむ連立方程式を解くこと 小 数係 をもつ連立方程式 解くこと かっこや係数に分数があ る




解き方 連立方程式の代入法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
この形の方程式を解くとき,普通の方程式を解くときの 「移項」のような変形をしにくい ので,解き方のコツを覚えておくとよいでしょう. 〇「 A=B=C 」というのは,「 A=B かつ B=C 」を省略的に書いたものです.だから,「 A=B=C 」という方程式が与えられ2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 (1) 答え 連立方程式の解き方 練習問題 (2) 答え 連立方程式の解き方 練習問題 (3) 答え 連立方程式の連立方程式(加減法1)_ 例題と練習 連立方程式(加減法2)_ 例題と練習 連立方程式(代入法1) 連立方程式(代入法2) 連立方程式



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




中学生 代入法のノート一覧 Clear
1連立1次方程式 1 2元連立1次方程式 \quad \begin {cases} a_1xb_1y &= c_1 \quad \cdots (1)\\ a_2xb_2y &=c_2 \quad \cdots (2)\end {cases} (1)、 (2)で1つの未知数を消去して1元1次方程式を導く。 消去の方法には、加減法、代入法、等値法がある。 ① a_1b_2a_2b_1 \neq 0 の時 連立方程式の解き方には「代入法」「加減法」の \(2\) 種類がありますが、どちらも上記の大原則に従っていると考えてください。 連立方程式の解き方 それでは、同じ例題を用いて代入法と加減法での解き方をそれぞれ見ていきましょう。 解き方①代入法連立方程式(計算練習2) 連立方程式を解け y=2x3 3xy=4 5xy=13 4xy=11 5x3y=19 4xy=11 x3y=8 x2y=7 5xy=9 y=2x5 4x7y=1 3x2y=8 2x3y=10 x=y5 12x04y=2 21x04y=46 3(4x2y)=x9 2x3y=6 4 3 x 5 4 y= 1 2 3 2 x 3 4 y= 9 2 1 4 x 1 2 y=1 2 3 x 8 9 y= 4 9 4x3y=2xy6=2




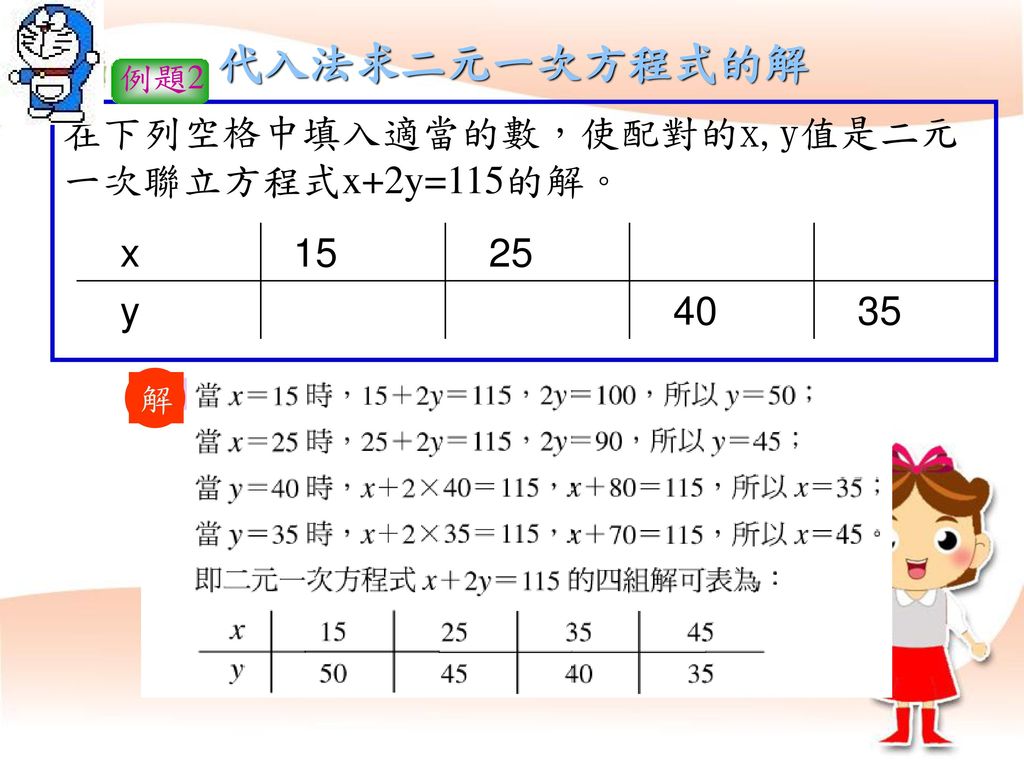
像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二
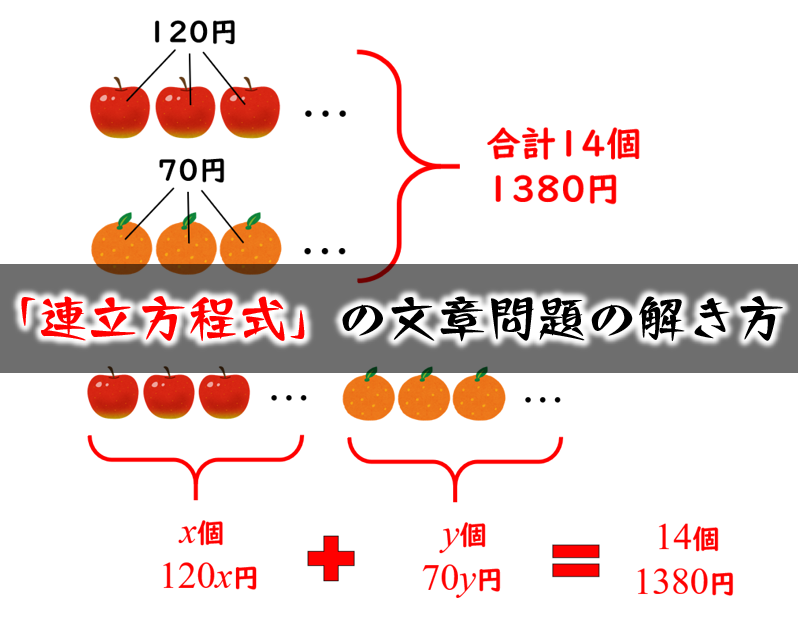



連立方程式の文章問題の解き方 数学fun
2つの文字 が含まれている連立方程式を解くには,加減法や代入法を使って,どちらか一方の文字を消去し,1つの文字だけの方程式に直して解くようにします. この問題のように の係数がそろっているときは,左辺どうし,右辺どうしを引くと を消去する『連立方程式』の単元から 連立方程式を 代入法で解く方法 について解説していくよ! 連立方程式を解くためには 『加減法』と『代入法』という2つの解き方があったよね。 でも 加減法は分かるけど、代入法は苦手連立方程式の問題を3問解説します。 目次 簡単な問題 例題1 代入法による答え 加減法による答え 普通の問題 例題2 加減法による解答




中学数学 連立方程式 加減法 中学数学の無料オンライン学習サイトchu Su




代入消去法1 Youtube
連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく代わりに入れる 連立方程式の解き方は\(2\) 種類です。 加減法と代入法です。 加減法はマスターしましたか? 続いて、連立方程式の解き方の2代入法を学習しましょう。 例題1 次の連立方程式を代入法基礎方程式の離散化 => 連立1次方程式(flow) Q数値解析とは? A 基礎方程式を離散化して最終的に得られる連立1次方程式を解く. 基礎方程式(1次元Laplace方程式) 差分方程式の代数表示 差分方程式 差分法で離散化 計算領域モデル 境界条件 連立1次方程式




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook
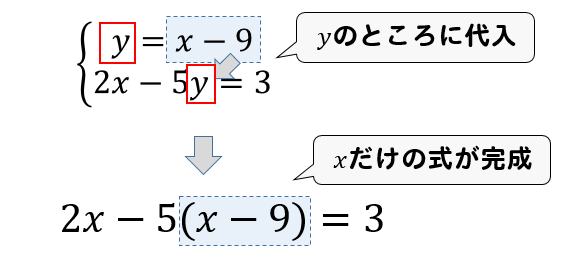



連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト
連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく連立方程式(加減法2) 連立方程式を解け x2y=1 4x3y=15 3x2y=8 2xy=6 5x6y=31 x7y=2 2xy=1 5x3y=1 2x3y=10 6x5y=26 5x6y=8 7x3y=5 12x5y=1 3x4y=37 11x10y=44 7x5y=13 2x5y=46 16x9y=4 5x7y=10 8x21y=33 6x5y=31例題:簡単な連立方程式 連立方程式の解き方を理解している人は、ここをクリックorタップしてください。 次の方程式を解け。 x2y=7 2xy=1 解き方は、代入法または加減法を使います。解き方別に紹介します。 加減法




用加減消元法解二元一次方程組 沒掌握的同學們請再學習一遍 每日頭條




連立方程式の解き方 の問題のわからないを5分で解決 映像授業のtry It トライイット




連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




中2です 加減法と代入法の違いがよくわからないんですが 教えてください 解き方も教 Clear




例題4 用代入消去法解二元一次聯立方程式3 Youtube




連立方程式 連立方程式の加減法と代入法 中学数学 定期テスト対策サイト




3分でわかる 連立方程式の代入法と加減法をわかりやすく 合格サプリ




二元二次方程式定義連立方程式とは Gjlni




連立方程式 A B C




聯立方程式聯立方程式 Qqkaii



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
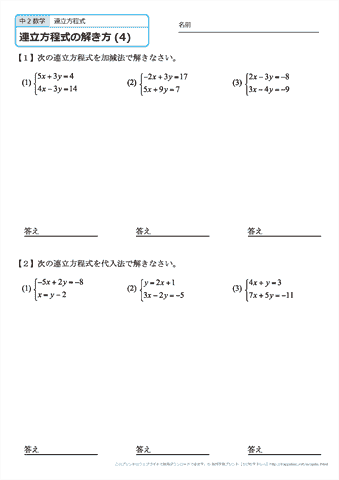



中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
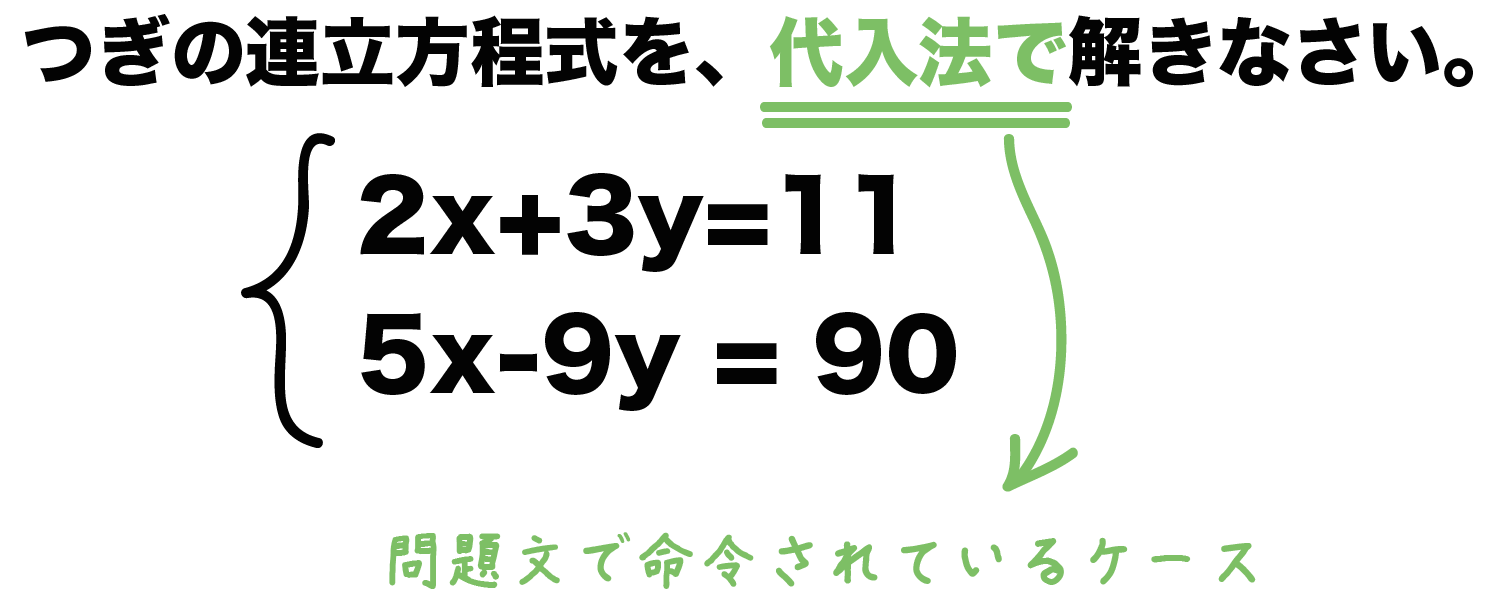



超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく




連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ




解き方 連立方程式の代入法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学2年 連立方程式 代入法 受験の月



Ex 加減消去法 基本 二元一次聯立方程式 發現學習的美麗新世界



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




70以上連立方程式代入法問題 ニーアオートマタ壁紙



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
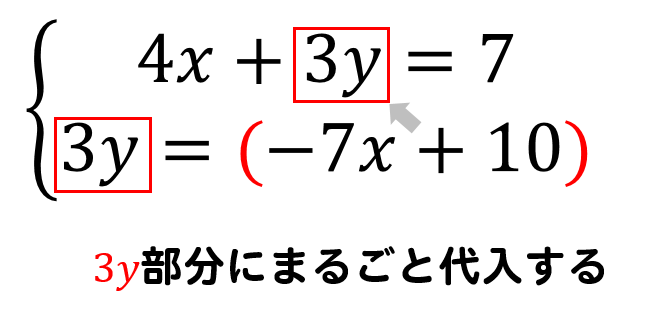



連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ




解き方 連立方程式の代入法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




数学の連立方程式のやり方が分かりません 教えてくれると有難いです Clear




連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




連立方程式 代入法の解き方をイチから解説 Youtube




Qnnhhgy 00r Pm



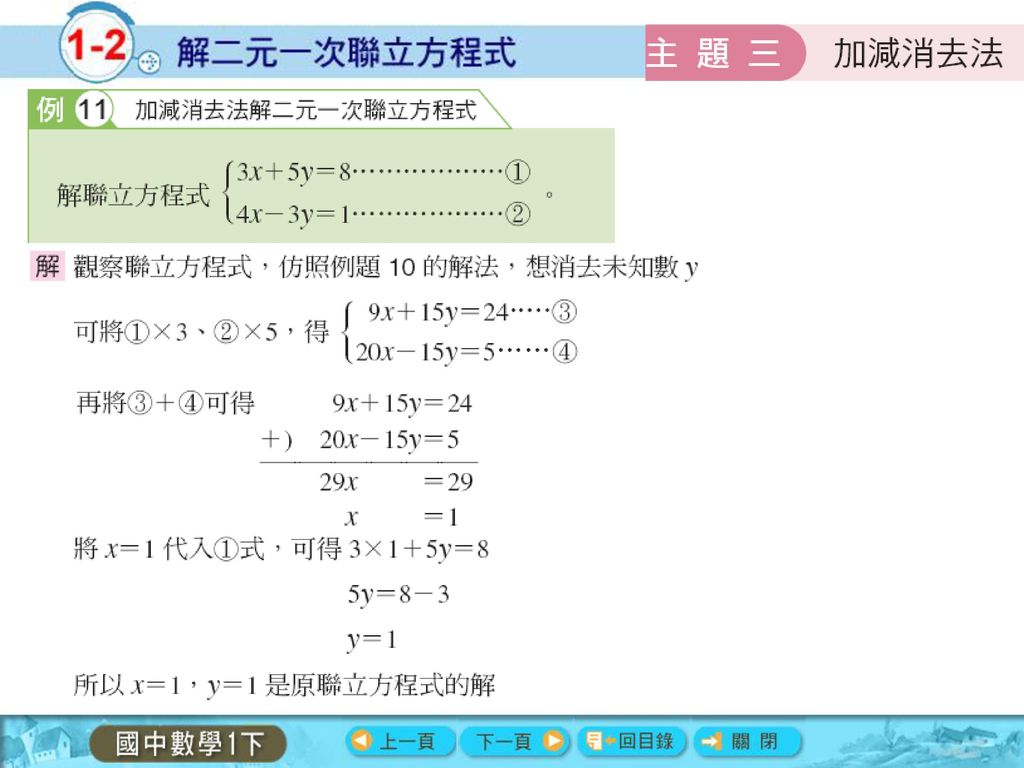
1 2 解二元一次聯立方程式主題一 二元一次聯立方程式主題二 代入消去法主題三 加減消去法重點整理新竹縣立湖口國民中學



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




連立方程式 加減法 代入法の簡単な練習問題 これでテストはバッチリ 数スタ




トップ100連立方程式公式 最高のカラーリングのアイデア




連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ



第1章 連立方程式



50 連立方程式例題 犬イラスト




中学数学 連立方程式 代入法 中学数学の無料オンライン学習サイトchu Su
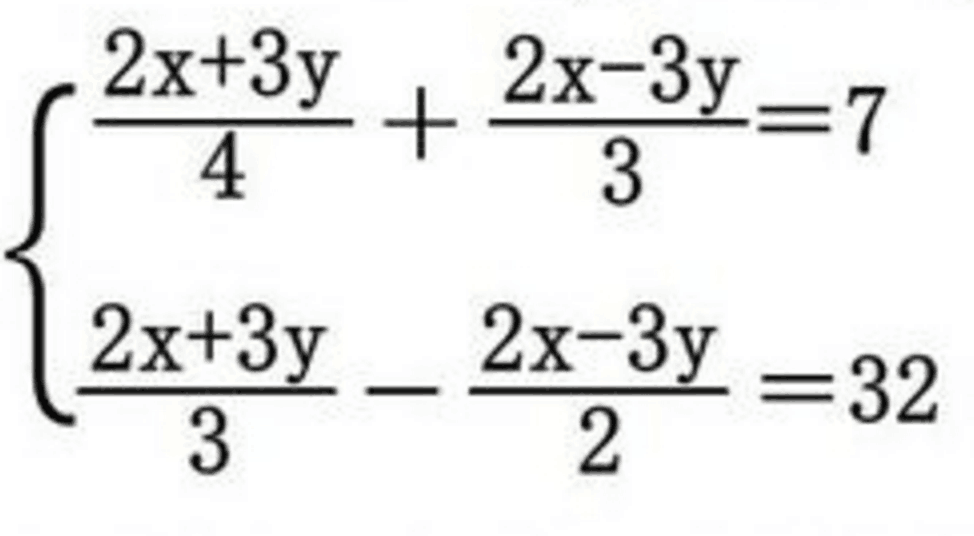



方程組 定義 解方程組的方法 1 代入法 2 畫圖法 3 消元法 例題 中文百科全書




1 2 解二元一次聯立方程式主題一 二元一次聯立方程式主題二 代入消去法主題三 加減消去法重點整理新竹縣立湖口國民中學



腾讯视频




中学数学 中学2年 Vol 0 連立方程式の解き方 代入法 Youtube




二元一次聯立方程式 代入消去法 Youtube



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




連立方程式の2つの解き方 代入法 加減法 数学fun




App Store 上的 中2連立方程式計算問題




連立方程式 1 代入法と加減法 バカでもわかる 中学数学




例題2 用代入消去法解二元一次聯立方程式1 Youtube



Http Eduweb Cy Edu Tw Tool Mothball 103 B S Module Download Update S File1221 2 Pdf




1 2 解二元一次聯立方程式主題一 二元一次聯立方程式主題二 代入消去法主題三 加減消去法重點整理新竹縣立湖口國民中學
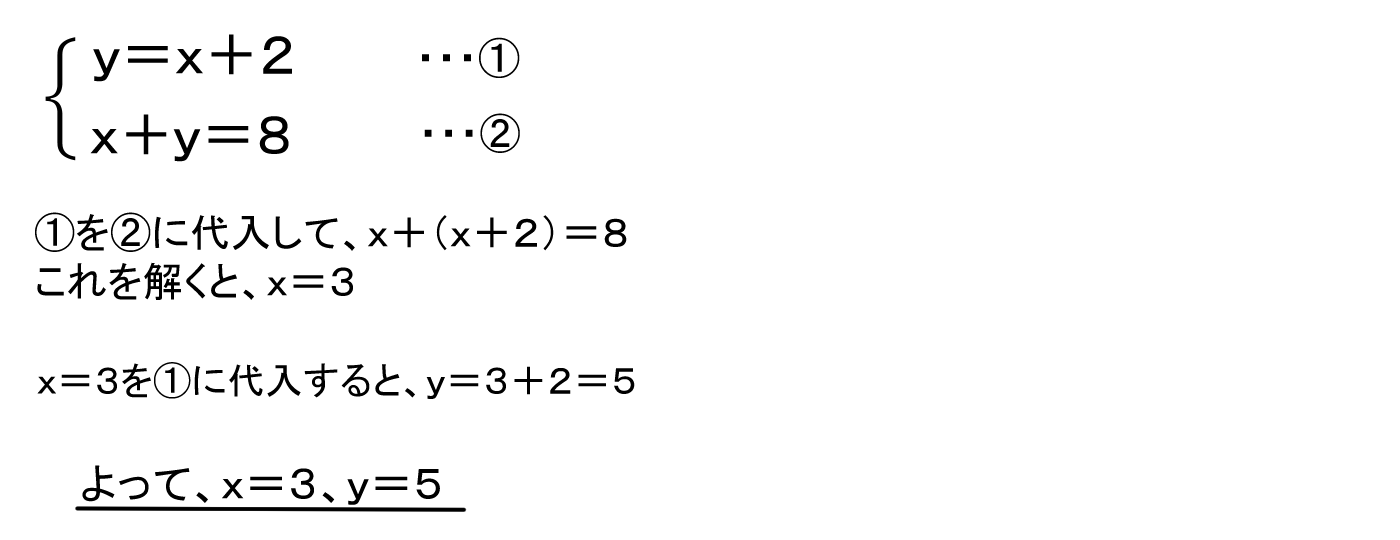



連立方程式 1 代入法と加減法 バカでもわかる 中学数学




05 代入消去法解二元一次聯立方程式 1 例題 Youtube




中学2年 数学 連立方程式 代入法 Youtube




連立方程式 代入法 無料で使える中学学習プリント




トップ100連立方程式公式 最高のカラーリングのアイデア



2




ม 2 โน ตของ 中2数学 連立方程式 ช น Junior High数学 Clear




均一影片 例題 代入消去法 Y Ax 學習單 Shareclass




数学 中2 17 連立方程式 代入法編 Youtube




超簡単 連立方程式の解き方を見分ける2つのコツ Qikeru 学びを楽しくわかりやすく




連立方程式の解き方 代入法




Kistenkasten723 数学では同じ問題の解き方にはいろいろな解き方があり それを発見できるのが楽しい これが数学の本質であり醍醐味なのだから それを1つに制限して 思考の自由を束縛するべきではない という批判がなされることがある




25 3 連立方程式 ニスヌーピー壁紙




中学生 代入法のノート一覧 Clear



腾讯视频
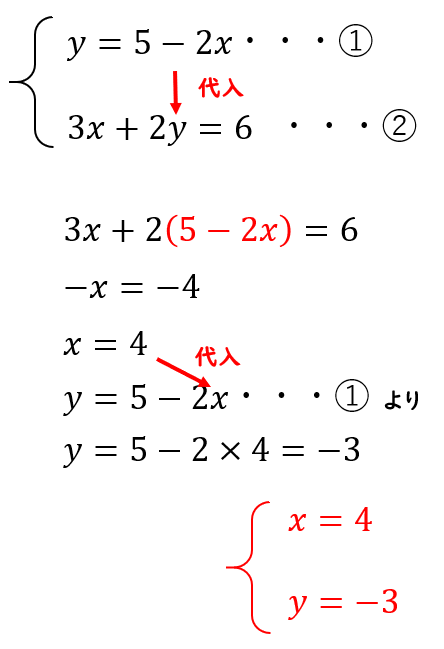



連立方程式の2つの解き方 代入法 加減法 数学fun




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




Junior High数学的連立方程式 2年 筆記 Clear




トップ100連立方程式公式 最高のカラーリングのアイデア
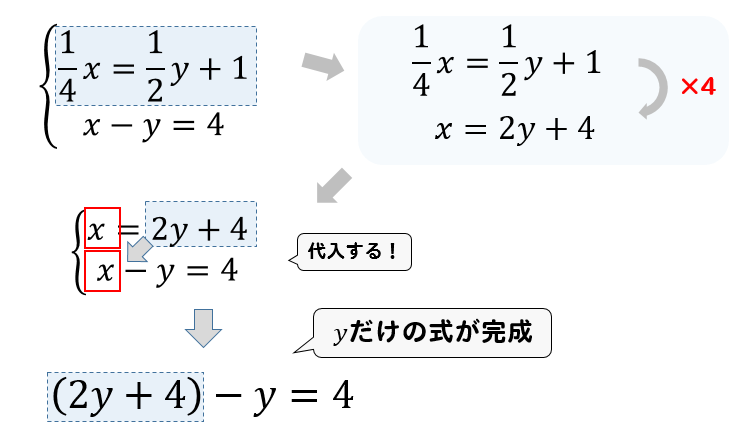



連立方程式 代入法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト



例 二元一次方程組及其解 台灣數位學苑 K12 數學




トップ100連立方程式公式 最高のカラーリングのアイデア
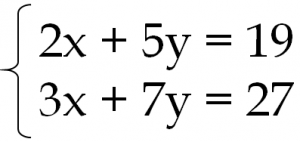



中2数学 連立方程式 代入法はこの3パターンで完璧 たけのこ塾 勉強が苦手な中学生のやる気をのばす




トップ100連立方程式公式 最高のカラーリングのアイデア




國二junior High数学的連立方程式の文章題筆記 Clear




高校数学で学習する連立方程式の解き方まとめ 数スタ




トップ100連立方程式公式 最高のカラーリングのアイデア




連立方程式 代入法 計算ドリル 問題集 数学fun




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




翻轉學習影片 國中 數學 二元一次聯立方程式及其應用問題



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
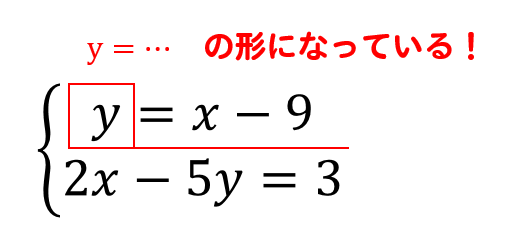



連立方程式 代入法の解き方をわかりやすく問題を使って徹底解説 数スタ




中2数学 連立法的式の代入法 例題編 映像授業のtry It トライイット



像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二




トップ100連立方程式公式 最高のカラーリングのアイデア




連立方程式の解き方 代入法 Youtube




連立方程式中2 犬イラスト




代入法で解く 問題 Youtube



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




中2連立方程式の解き方と計算問題 代入法と加減法 Irohabook



代入消去法 台灣數位學苑 K12 數學



0 件のコメント:
コメントを投稿