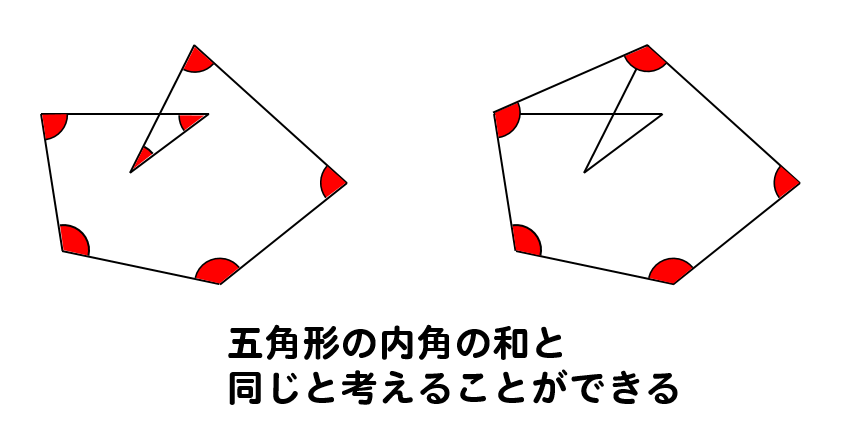
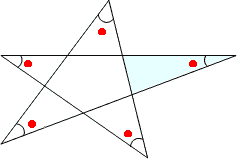
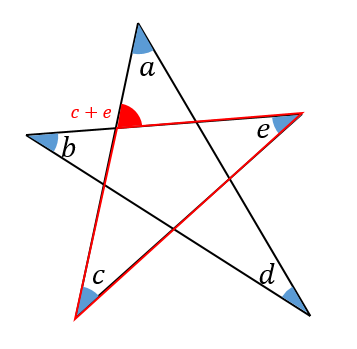
角の和は何度でしょう。 どんな星形五角形でも印をつけた5つの角の和は180°に なる。その理由をできるだけ多くの方法で説明してみよう。 ①ブーメラン型の図形 の角度を利用 ②補助線を引く⇒三角形 の内角の和4/8/13 図形ドリル 算数星人/カワタケイタ 第4問 正方形の角度 図形ドリル 45度 5年生 6年生 正方形 角度 角度の和 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。せ、図形の持つ不思議さや美しさも体感させていきたい。 レディネステスト問題内容 正答 誤答(無回答含) 角の性質や半回転の角度、4直角の角度を求める問題 12人(75%) 4人(25%) 三角形の弁別を問う問題 14人(%) 2人(12%)
3
図形の角度の和
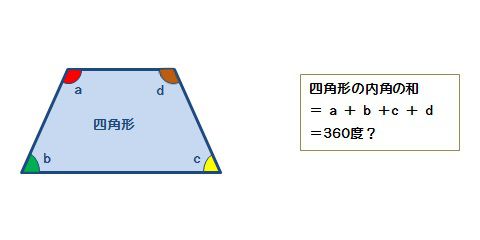
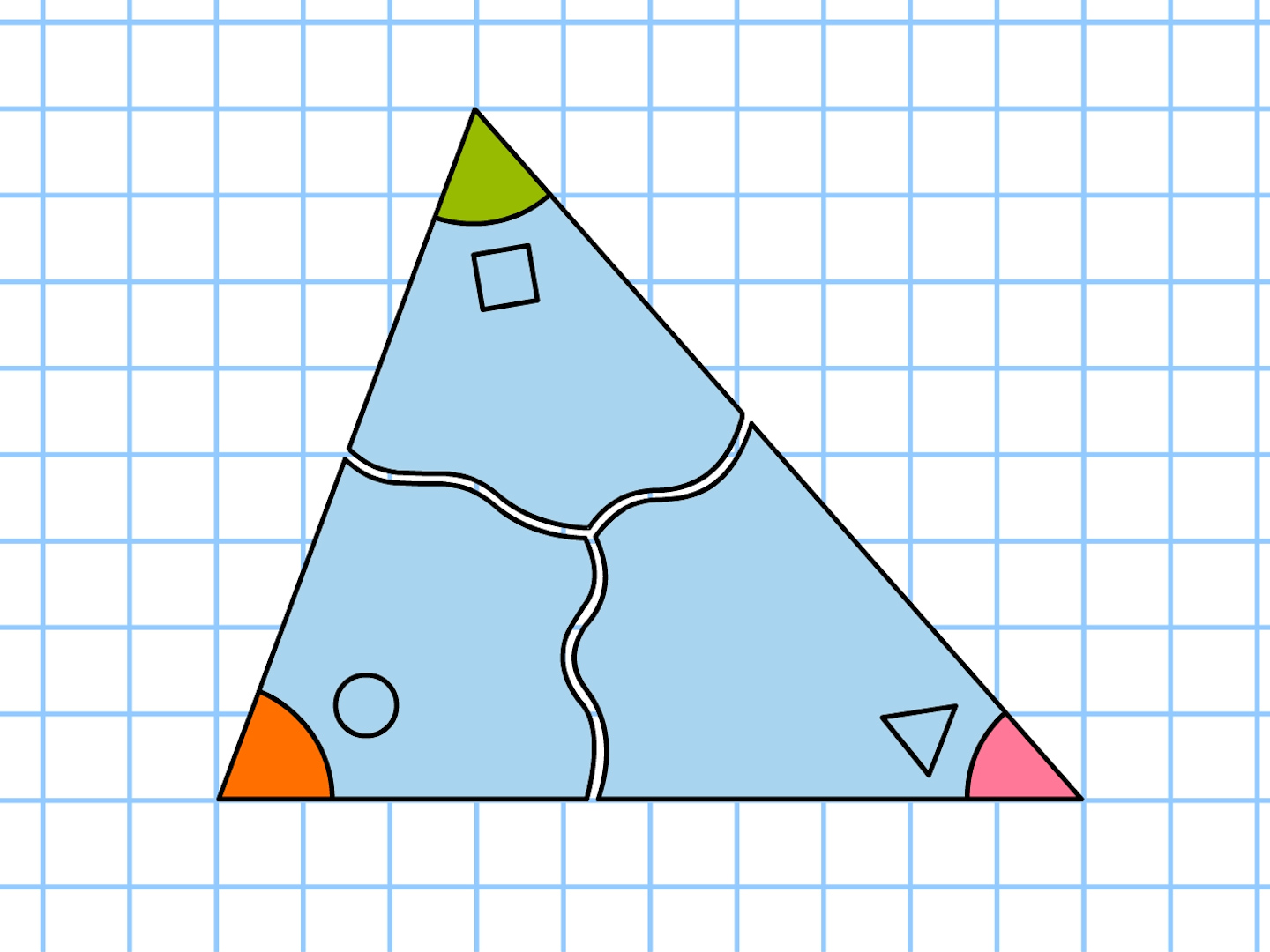
図形の角度の和-数量や図形についての表現・処理 (4) ・三角形の内角の和が180°であることや,多角形の内角の和は三角形に分割することによって 求められることを理解する。 ・正多角形の概念やその作図の仕方を理解する。 数量や図形についての知識・理解 三角形の内角の和が180°であることを理解する。 ※合同な図形を敷き詰めたもようを観察したり、3つの角を集めたりする活動。 習得 10 三角形の内角の和が180°であることを使って未知の角の大きさを求める事ができる。




多角形の内角の和 算数の公式覚えてますか
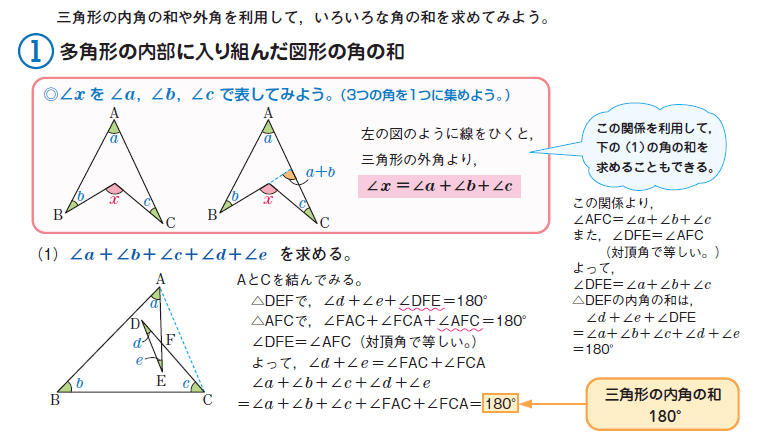
Afj, bgf,等の5つの三角形の内角の和から,五角形の外角の和2つ分を引いて, 180×5-360×2 =180° 外側の五角形から付け足した三角形5つ分を引き,内側の五角形をたすと, 180×(5-2)-180×5 +180×(5-2)=180°問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答三角形の内角の和や外角を利用して,いろいろな角の和を求めてみよう。 多角形の内部に入り組んだ図形の角の和 2 多角形の内角の和の利用 (1)~(3)の図形の角の和を求めよう。 ∠x を ∠a,∠b,∠c で表してみよう。(3つの角を1つに集めよう。
入試解説 6年生 男子校 5年生 正方形 正三角形 東京 兵庫 灘 算数オリンピック 共学校 面積比 円 図形NOTE logix出版 角度 1日目 直角三角形 4年生 女子校 相似 立方体 長方形 おうぎ形 30度 正六角形 16年 17年 19年 トライアル 18年 年 ファイナル 二等辺三角形 直角二等辺三角形 21年 立体の切断 15年 図形の移動 共通部分 大阪 面積の和 12年 13年 3年生 ジュニア(1) 三角形の内角の和は180°に等しい. (2) 三角形の外角は,それと隣り合わない2つの内角の和に等しい. ≪例≫ (1) 上の図において ∠A∠B∠C=180° (2) 上の図において ∠ACD=∠A∠B①三角形、四角形の内角の和を確認する ②三角形、四角形の外角を知り、外角の和が360°を確認する 到達目標 平面図形の内角や外角を理解する
内角の和が180°になるということがわかります。 星形の図形では 三角形の外角の性質を利用していくと 全ての角を1つの三角形に集めることができるので 最終的には、和が180°!ということになります。正五角形の角度(筑波大学附属中学 07年算数入試問題) 角度は何度?(中学受験算数 平面図形) 7つの角度(中学受験算数 入試問題研究) なぜ角度の和を求めるのかがヒント!(早稲田中学 10年4/4/19 正六角形は対角線で、4つの三角形に分かれるので、内角の和は、 180×(6-2)=7度 正六角形の角は全部で6つあるので、1つの角の大きさは、 7÷6=1度 で求められます。




数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局



みんなの算数オンライン 中学受験 4年 平面図形 角度2 角の和 トレーニング
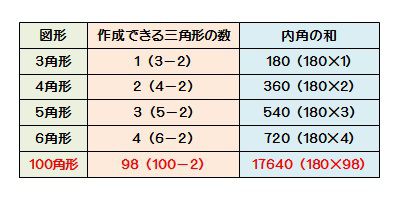
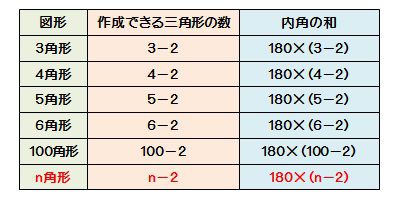
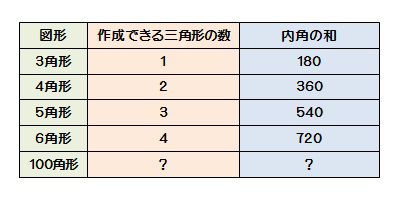
関心・意欲・態度 図形の性質に関心を持ち,調べようとしたり,三角形や四角形の角の大きさ の和について,筋道立てて考えようとしたりしている。 数学的な考え方 三角形の三つの角の大きさの和が180°であるという性質を帰納的に見いだ三角形の数で内角の和が計算できます 五角形と六角形の内部に作成できる「三角形の数」「内角の和」は下の図の通り。 四角形と同じように、三角形の数が分かれば内角の和は求められますよね^^ どうですか? ここまではそれほど難しくないと思います。 多角形と言っても、まだまだ五角形、六角形と数が少ない形ですからね。 ということで! ここで一気に四角形ではそれが4組あるので、図の赤と青すべての角の和は180×4=7 青の角は内角なので四角形の内角の和360 赤と青の和7から青の和360を引くと7360=360 よって四角形の外角の和は360°となります。



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
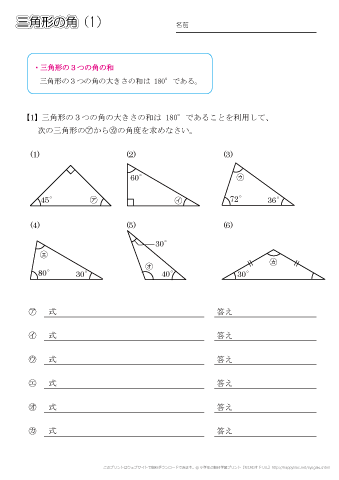
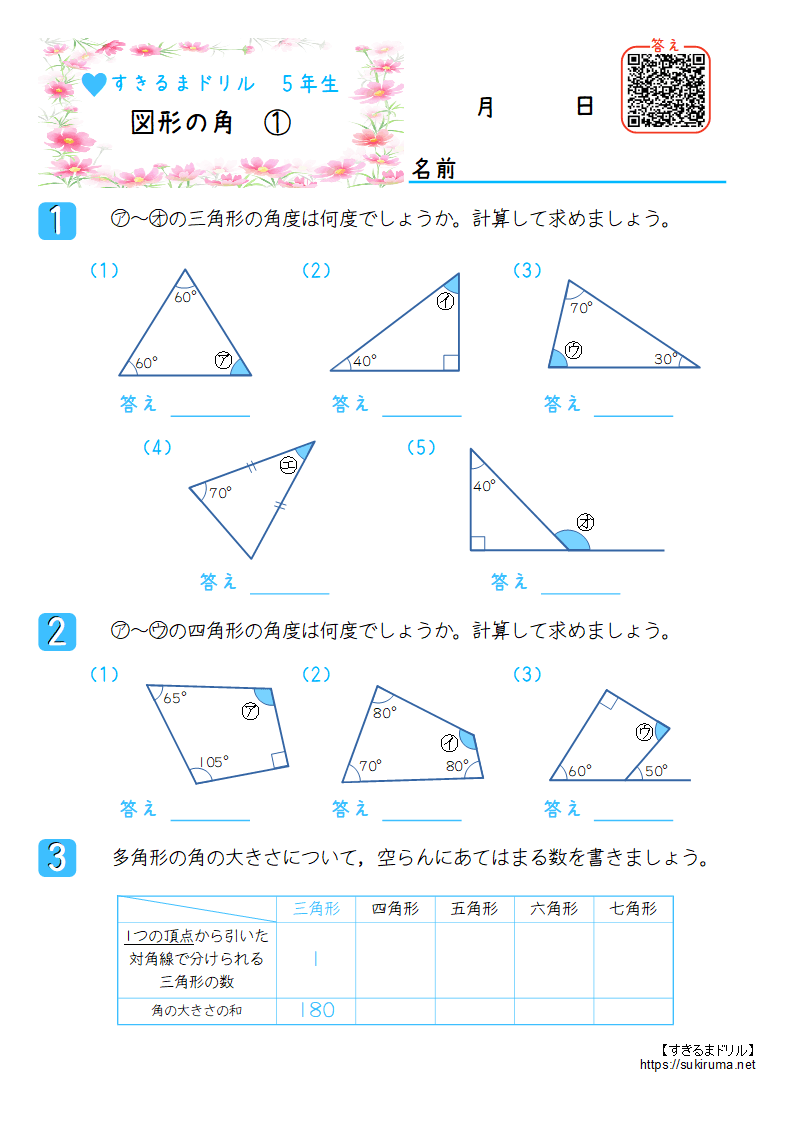
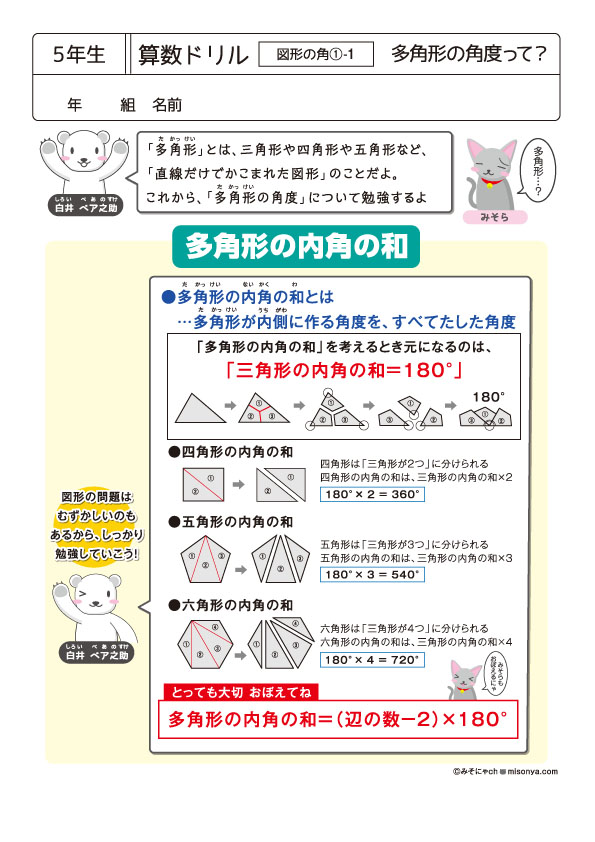
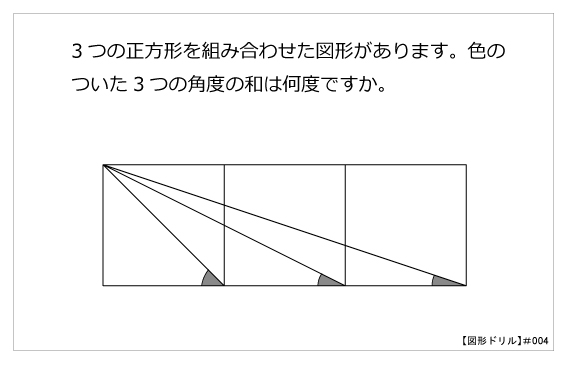
㋐~㋒の四角形の角度は何度でしょうか。計算して求めましょう。 答え 答え 答え 多角形の角の大きさについて,空らんにあてはまる数を書きましょう。 三角形 四角形 五角形 六角形 七角形 1 角の大きさの和 180 すきるまドリル 5年生 (1) (2) (3)前時の星形五角形の頂角の和を求める 授業では、作図をして角度を求めさせ、 頂角の和が1800であることを多様な方 法で証明させた。かなり難しい内容なの で、6種類のヒントプリントも用意して、 理解の促進を図った。様々な証明方法の内角の和は 180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い




星形図形の角度の和は 中2平行と合同12 Youtube



多角形の内角の和 算数の公式覚えてますか
和について演繹的に考え,四角形の性質としてとらえることができる。 数学的な考え方 三角形や四角形の内角の和を用いて,未知の角度を計算で求めることができる。 数量や図形についての技能3/1/19 \(n\)角形の内角の和は「\(180°×(n2)\)」でしたが、「\(n2\)」というのは分割できる三角形の数と見ることができるのです。 そしてそれぞれの多角形の内角の和はすべての三角形の内角の和と等しいので、 「\(180°\)×(三角形の数)」 というのが公式となります。中学受験 4年 unit 262 平面図形‐角度2 角の和 砂時計形に着目! 角度の和① 4年生向け 中学受験 算数 角の和 対頂角が等しいことを利用して角度を求めます。 例題とともに解説します。 If playback doesn't begin shortly, try restarting your device Videos you watch



内角の和 算数用語集



小学5年生 算数 無料問題集 多角形の角の大きさ おかわりドリル
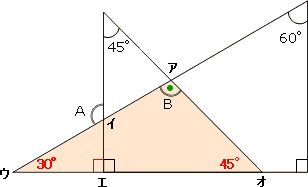
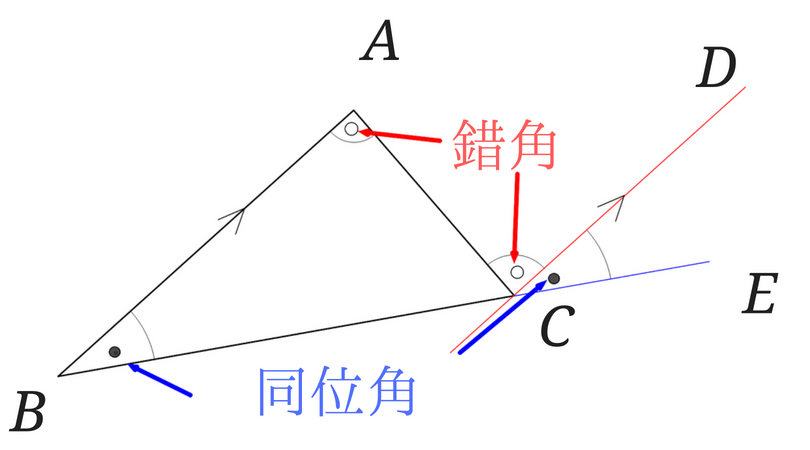
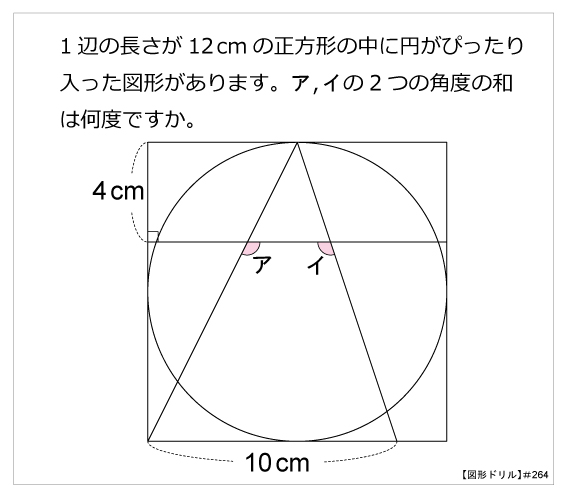
1/8/19 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質図形ドリル 算数星人/カワタケイタ 第264問 正方形と角度の和 図形ドリル 5年生 6年生 正方形 角度の和 ★★★★☆☆(中学入試難関校レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。黒い角度の和は180度。 答( 180 )度 下の図の赤い三角形に,外角の定理を使う。 χ=+25=45(度)。 答( 45 )度 星形の角度を求めるのに便利 な公式を利用すると,右の図の 2つの白い角度の和は,黒い2 つの角度の和と等しいことがわ かる。



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント




課題学習の指導 数学
算数 中学入試対策B①/図形の折り返しと角度 ラーニング 1 例題1 解き方 《1.図形の折り返し》 図は長方形を折り返したものです。アの角の大きさは何度でしょう。 折り返したことから,図の と , と はそれぞれ同じ角で,大きさは等しいです。星型 角形の角度の問題 今日は、星型 角形の角度について,紹介します。 まずは,問題に挑戦してみてください! 図の5つの角度ア~オの和を求めなさい。 となります。 図の7つの角度ア~キの和を求めなさい。 例題のような一筆書きした図形を「 星形長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 » この記事の続きを読む 多角形の内角の和




図形ドリル 和が45度になる角 受験算数に挑戦



1
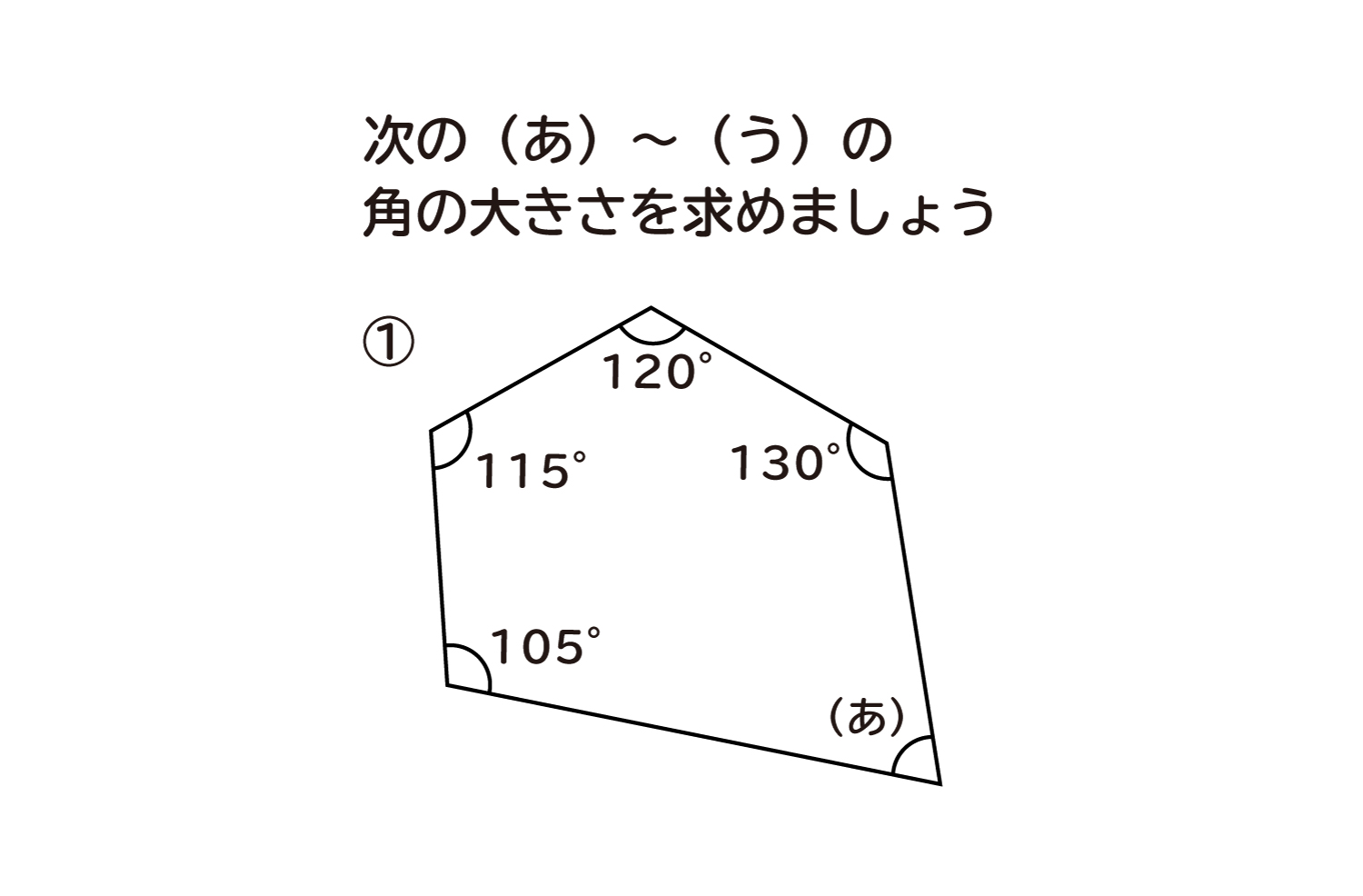
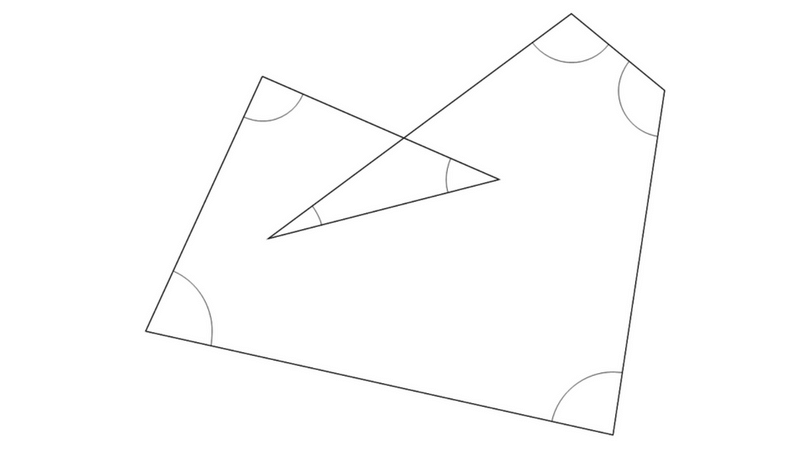
画像の図形の内角の和は900度なのですが 求め方が分かりません。 答えの式には180(72)=900 となるのですが、なぜ七角形になるのでしょうか? 分かる方ご回答お願いします。内角の和を考える方法 次は内角の和から1つ分の大きさを求める方法です。 まず、多角形の内角の和は $$\LARGE{180 \times (n2)}$$ で求めることができましたね。 正三角形の内角の和であれば $$\LARGE{180 \times (32)=180°}$$いろいろな方法で星形五角形の頂点の和を求めることや星形六角形,星形七角形,星形八角形,の頂角の和を次々と求めて,いくつかの規則性を発見することは,実に興味深いテーマである。 生徒自らが意欲的に,しかも,探究的に学習を進めることのできる課題学習に適した教材であると考える。 2.授業の実際 ・ 題材 「星形多角形の秘密」(2年) ・ 単元




印がついている角の和を求めなさい という問題の解説の意味がわからないです Clear




ペルソナ5 星形の図形のa Eの角度の和の答え 7月9日数学の宇佐美の授業編 P5攻略 元プログラマーぷげらの趣味ブログ
図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し図形の名前 三角形 四角形 五角形 六角形 七角形 八角形 九角形 ・・・ 二十角形 三角形の数 1 2 3 4 5 6 7 ・・・ ―2=18 求める式 ・・・ 内角の和 180° 360 7° 900° 1080° 1260° ・・・ °




多角形の内角の和 算数の公式覚えてますか




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



図形の角の和 中学受験 早期英才教育 さくら教育研究所 Skredu



変形多角形の 内角 名寄 算数数学教室より



角度の求め方 算数の教え上手 学びの場 Com



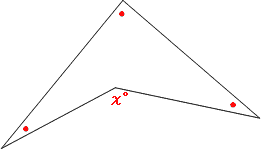
ちょうちょ型図形の角度は 求め方を徹底解説 数スタ




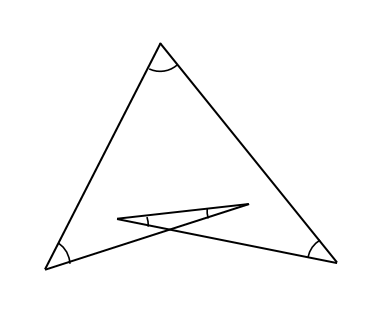
中学数学より1 星形5角形の内角の和 身勝手な主張
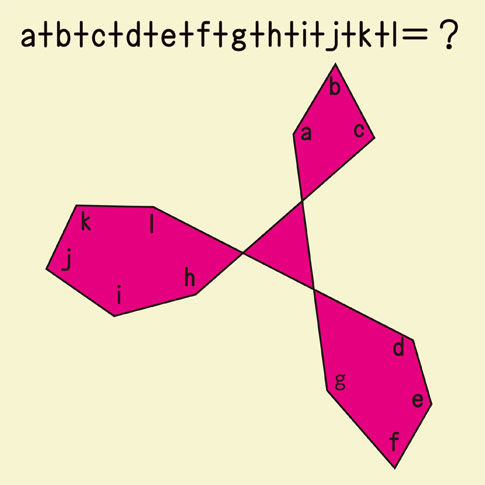



12個の角の和を求められますか 油断大敵を地で行く問題 秒刊sunday



1
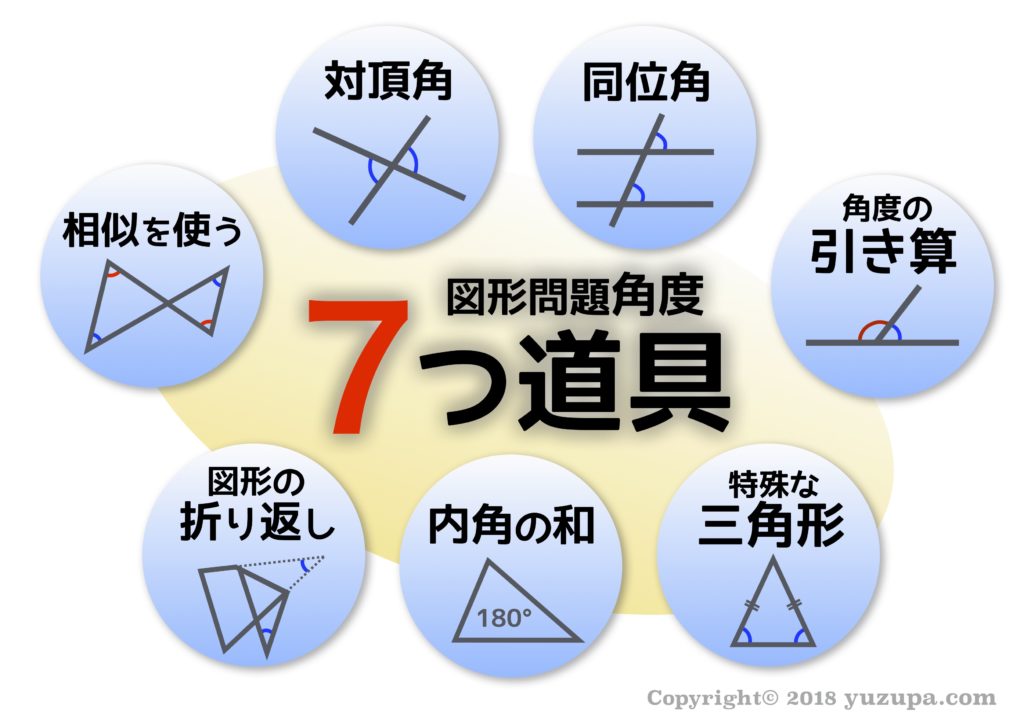



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋
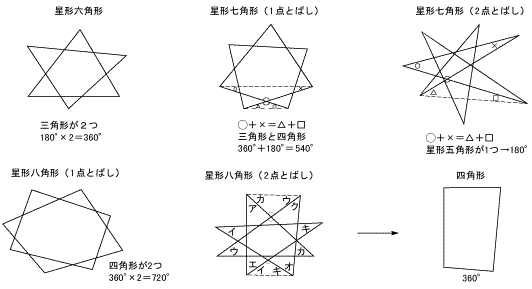



課題学習の指導 数学



ちょうちょ型図形の角度は 求め方を徹底解説 数スタ



四角形の内角の和 算数の公式覚えてますか



星形の図形の角度の和が苦手なので 教えてほしいです 中学数学 Yahoo 知恵袋



角度の求め方 算数の教え上手 学びの場 Com



無料の学習プリント 小学5年生の算数ドリル 図形の角1 みそにゃch




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




中2数学 複雑な多角形 角の和 応用問題



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題



平面図形の角度 第28問 角度の和 浅野中学 03年 甲陽学院中学 02年 入試問題 算数 まいにち一題 中学受験過去問題研究



多角形の内角の和 算数の公式覚えてますか



5年 三角形のふしぎ 算数イメージ動画集 大日本図書
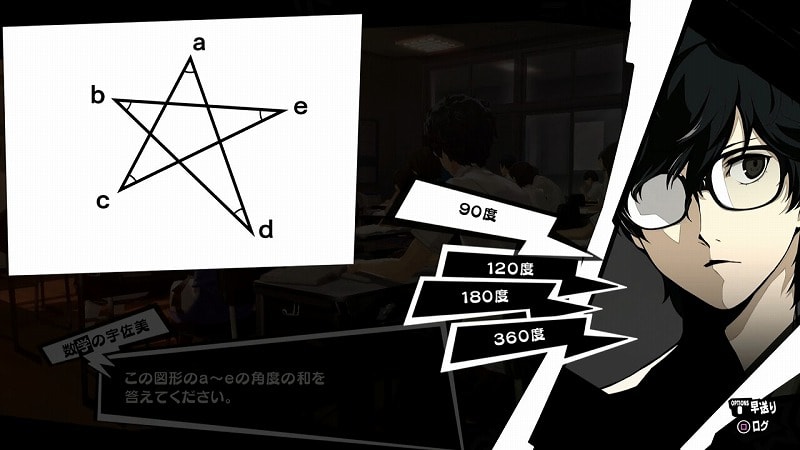



ペルソナ5 星形の図形のa Eの角度の和の正解 答え P5攻略ブログ 狩りゲー島




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学



3分でゲット 八角形の内角の和がわかる公式 Qikeru 学びを楽しくわかりやすく




印のついた角度の和を求めろ という問題です 解き方がよくわかりません Clear




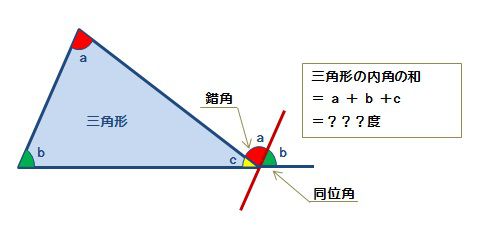
三角形の内角の和が180 になることの証明 数学fun



ア キの7つの角度の和は 開智未来中学 2012年 中学受験ー算数解き方ポータル



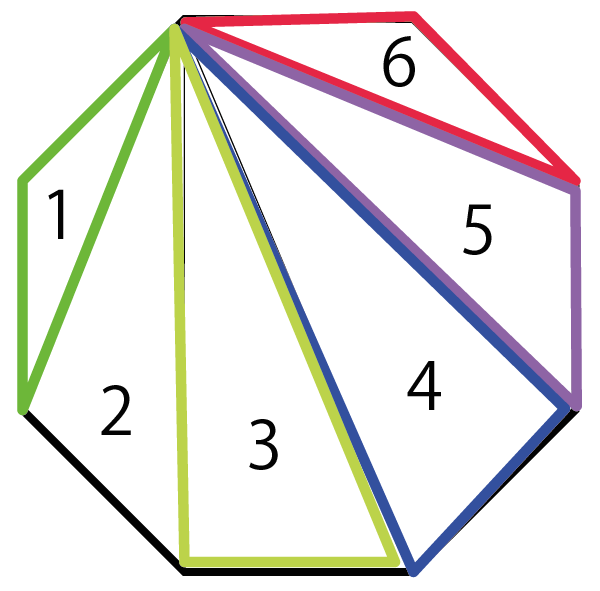
角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦



角度の求め方 算数の教え上手 学びの場 Com




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



多角形の内角の和 算数の公式覚えてますか



多角形の内角と外角 思考力を鍛える数学



3




角度 8 図形問題 算数 多角形 和 早稲田中学校 中学受験 Youtube




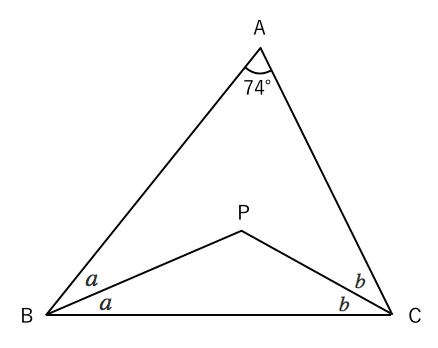
星形の先端の角の和が180 になる理由を教えてください Clear
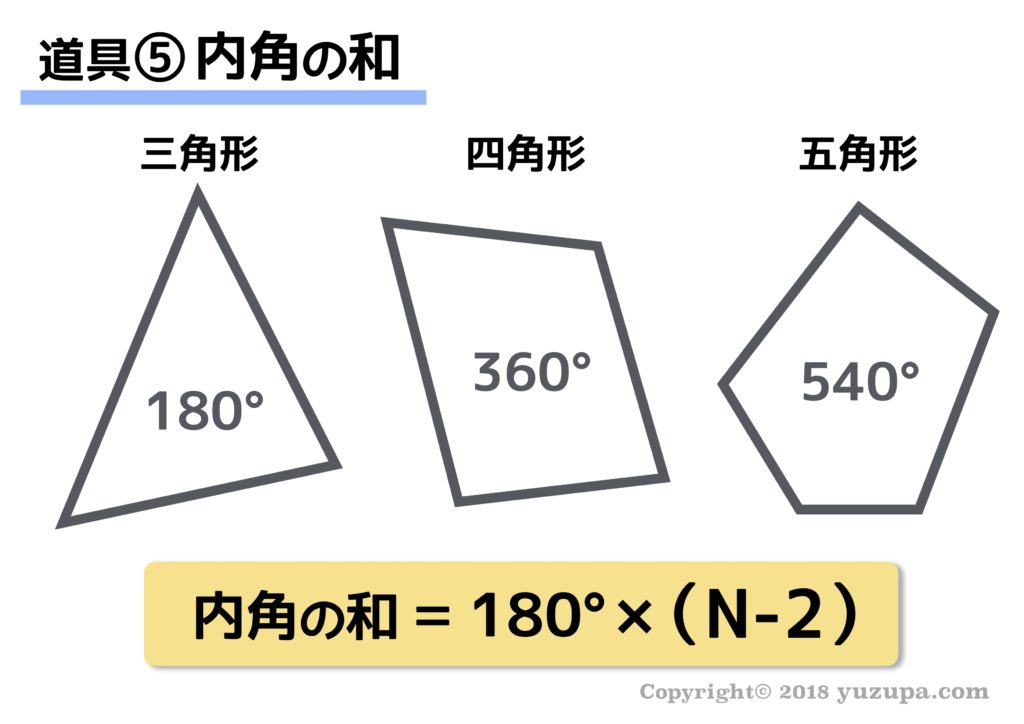



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋




図形ドリル 和が45度になる角 受験算数に挑戦
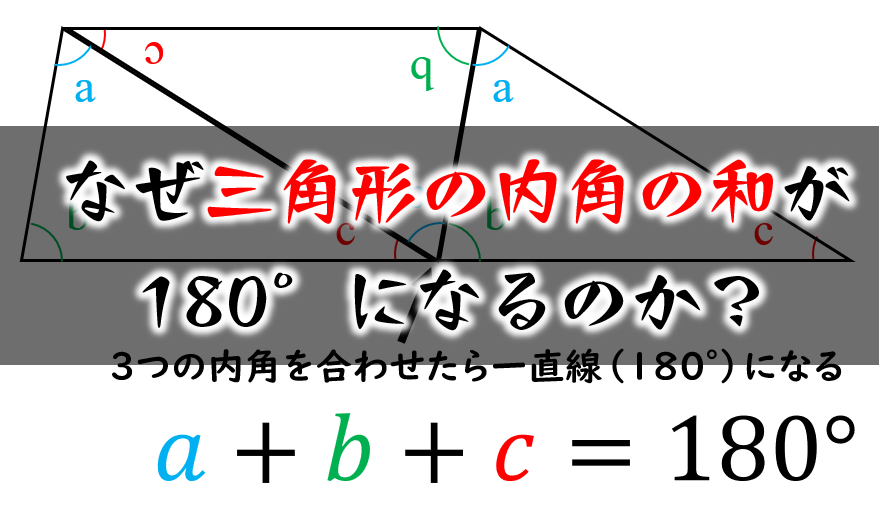



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




内角の和 180 N 2 外角の和 360 教遊者
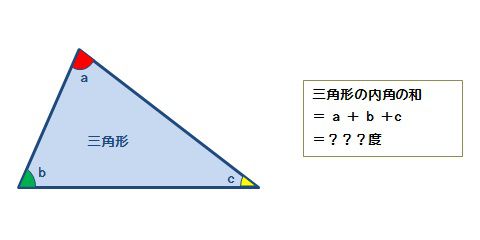



三角形の内角の和 算数の公式覚えてますか



なぜ星型七角形の角の和は540 になるのでしょうか 中2でも分か Yahoo 知恵袋




多角形の内角の和 外角の和の公式 数学fun
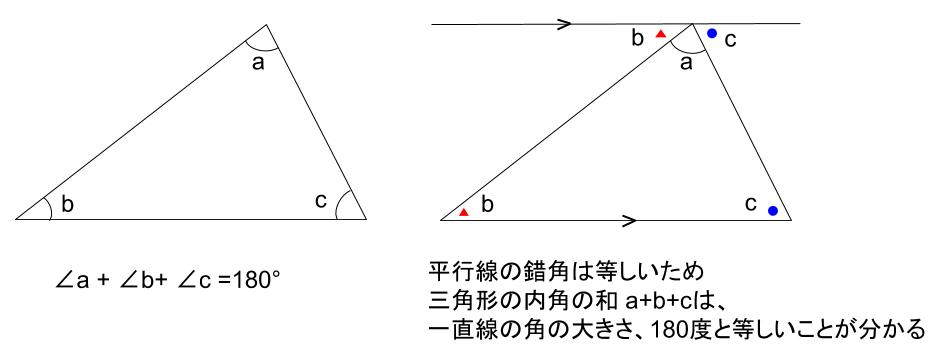



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




中2数学 複雑な多角形 角の和 応用問題
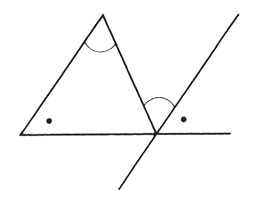



内角の和 算数用語集




中学2年生の数学 内角の和 外角の和の復習 塾講師が数学をやりmath
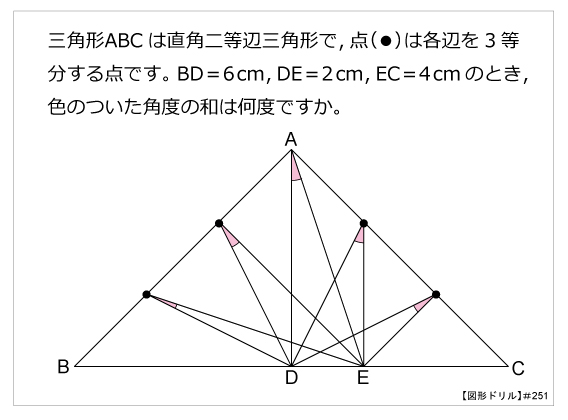



図形ドリル 第251問 5つの角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦




星型 角形の角度の問題 恋する中学受験 大学受験を見据えた中学受験
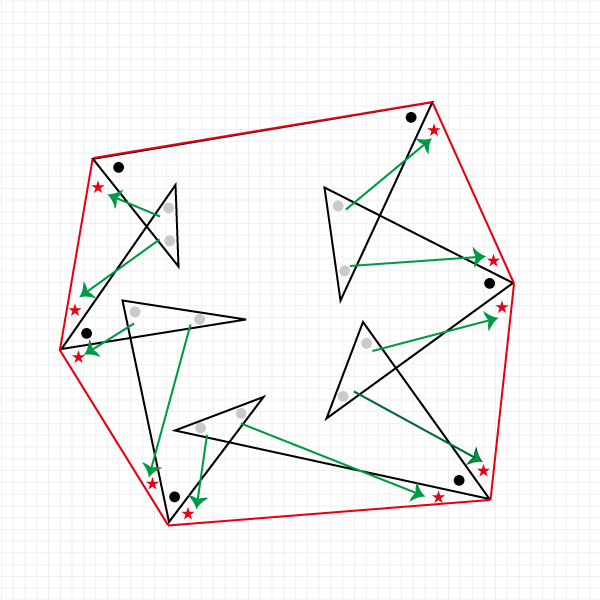



角度情報がない図形の合計の角度 星形多角形 受験算数入門




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




星形多角形 頂角の和 星形七角形まで 中学2年数学から Youtube




小学校5年 算数 四角形の内角の和 Youtube
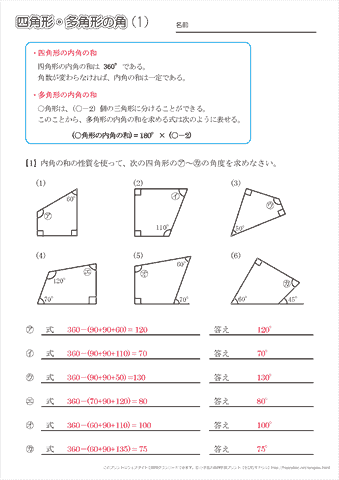



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
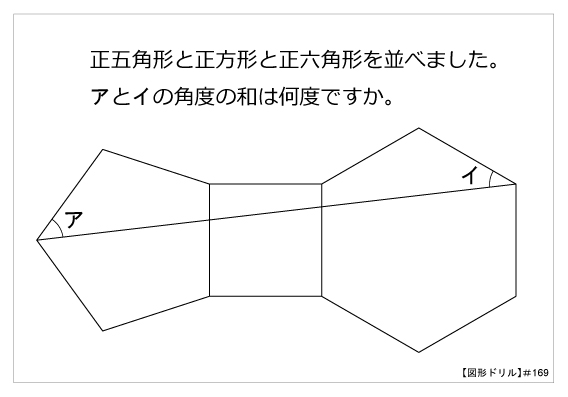



図形ドリル 第169問 角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
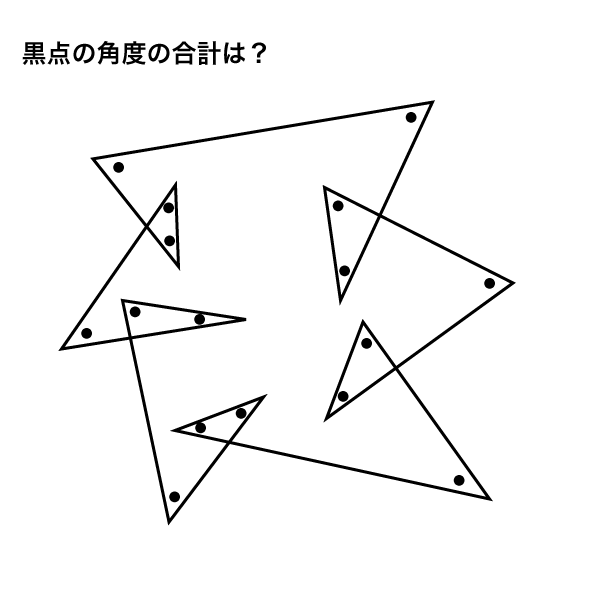



角度情報がない図形の合計の角度 星形多角形 受験算数入門
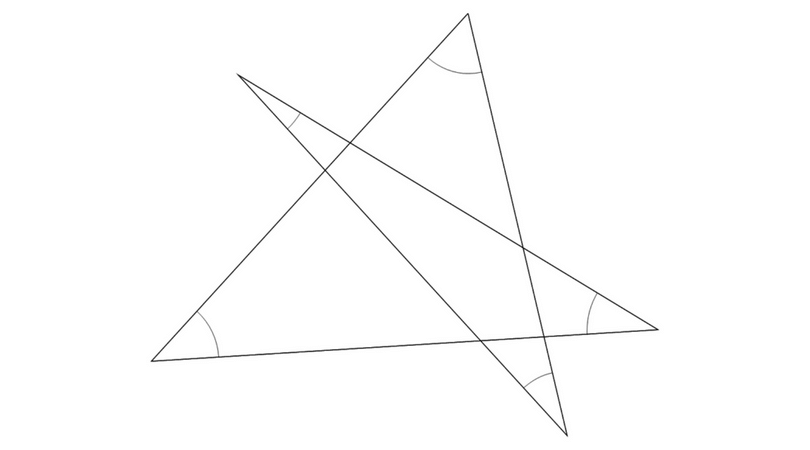



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局




多角形の内角の和 外角の和の公式 数学fun
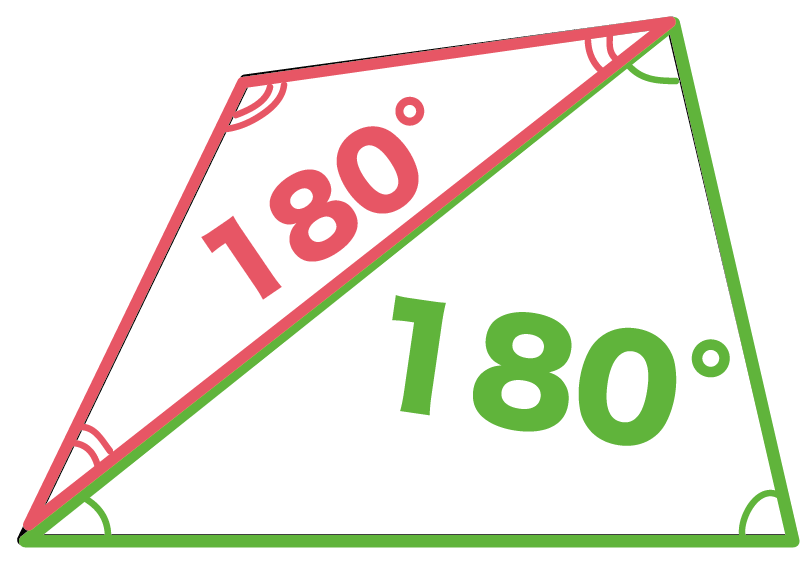



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



星形の角度 内角の和の求め方を問題解説 数スタ




図形 角度の求め方 中2 画像の図形の内角の和は900度なのですが 求め Okwave



角度問題より 多角形の内角の和 大宮開成中学 2010年 これが中学入試に出た図形問題



角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




中2数学 ブーメラン型角度の求め方を解説 数スタ



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局



2 48 第3章 多角形の角 いろいろな図形の角 Kakera Link 公式ブログ




多角形の内角の和 は何度なのか を説明します おかわりドリル



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
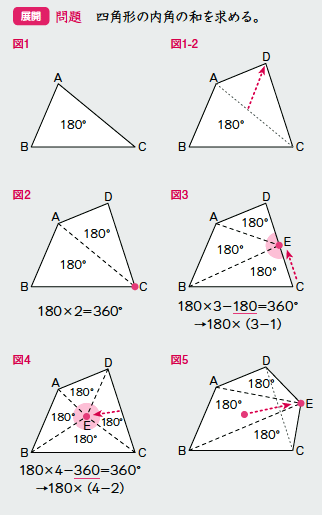



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



5年 四角形のふしぎ 算数イメージ動画集 大日本図書




中学数学 求角 一筆書きの角度 中学数学の無料オンライン学習サイトchu Su




内角の和 180 N 2 外角の和 360 教遊者



三角形の内角の和 算数の公式覚えてますか
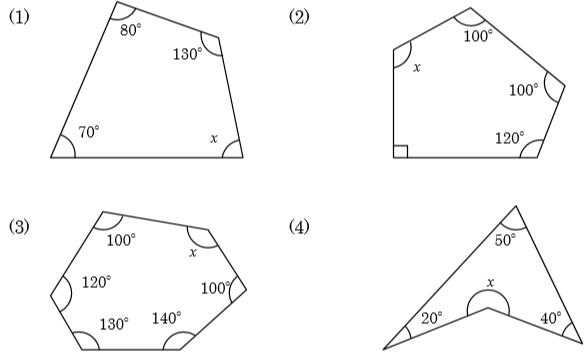



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




星形の角度 内角の和の求め方を問題解説 数スタ
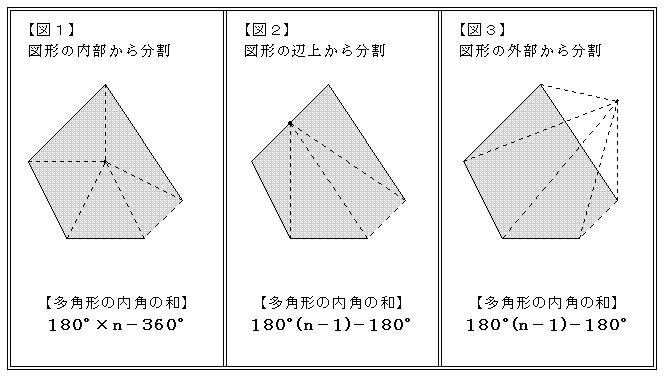



多角形の角
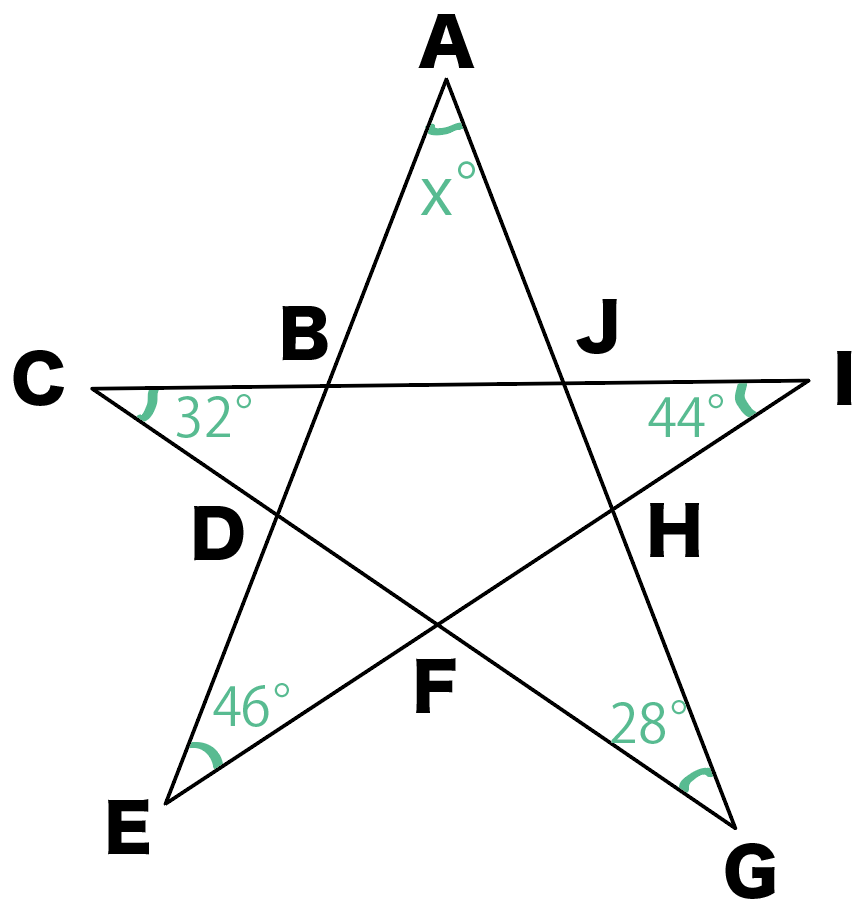



星形の角度の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




多角形の内角の和 は何度なのか を説明します おかわりドリル
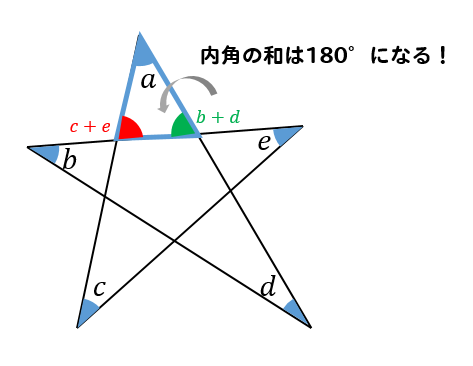



星形の角度 内角の和の求め方を問題解説 数スタ



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



3




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
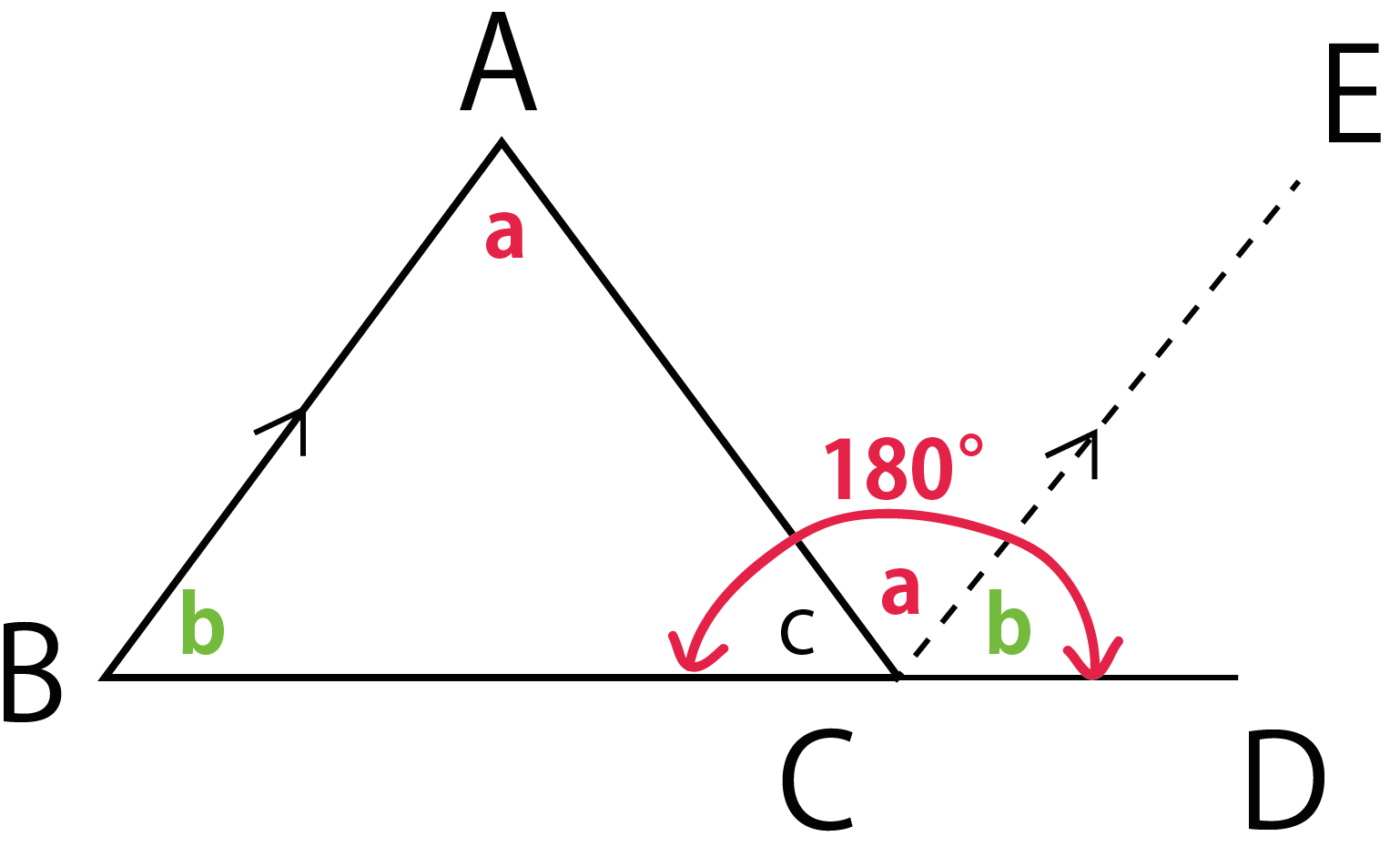



中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿