多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun 数学 中2 51 多角形の内角と外角の和 基本編 Youtube 正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく 四角形の内角の和 算数の公式覚えてますか四角形ではそれが4組あるので、図の赤と青すべての角の和は180×4=7 青の角は内角なので四角形の内角の和360 赤と青の和7から青の和360を引くと7360=360 よって四角形の外角の和は360°となります。特徴 一般的には矢型、楔型などで呼ばれる。 四角形abcdにおいて、∠a,c,dの合計が角bの外角に等しくなる。 また、点bを中心とする円が点a,c,dに内接する場合、∠bの外角は∠dの2倍である。 証明 点d,点bを結び、∠bdcを∠f,∠cbdを∠l,∠bdaを∠h,∠abdを∠s,∠bの外角を∠xとすると、
3
四角形の内角の和 公式
四角形の内角の和 公式-多角形の内角の和と問題の求め方 十角形の内角の和を求めましょう。 辺の数が分かれば上記の公式を使って簡単に解ける問題です。 n=10なので 多角形の内角の和=180× n-2=180× 8=1440° 内角の和と三角形の関係は? 1分でわかる和の値、証明、外角との関係四角形の内角の和算数の公式覚えてますか? 四角形の種類と定義・性質の違い正方形・長方形・平行四辺 凹四角形 Wikipedia;




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題
星型八角形は四角形が2つ(7°),星型十角 形は五角形が2つ(1080°)の図形の組み合わせ であり,その内角の和は容易に求められる。 星型多角形の内角の和を次の表にまとめた。 この表から,星型多角形の内角の和は,頂点の性質1の逆も成立します。つまり, 向かい合う内角の和が 18 0 ∘ 180^{\circ} 18 0 ∘ である四角形は円に内接します。 また,性質1は「外角」を使って表現されることも多いです。こんにちは、ウチダです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください♪ 多角形の内角の和・外角の和
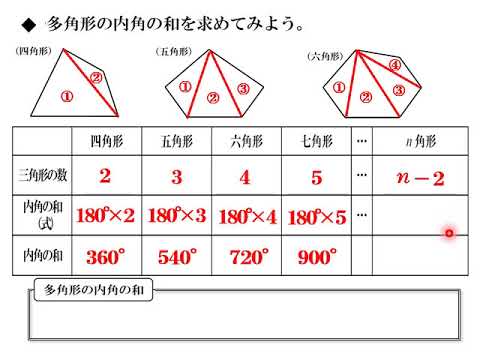
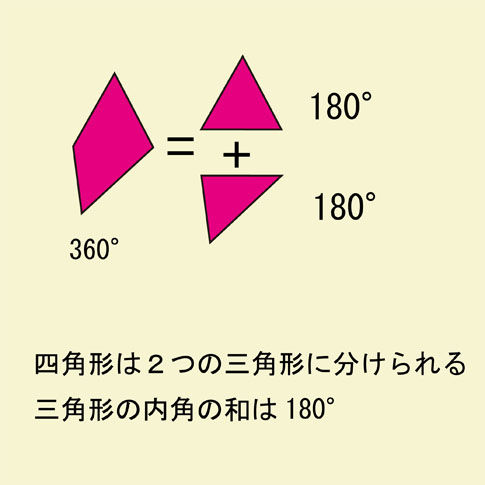
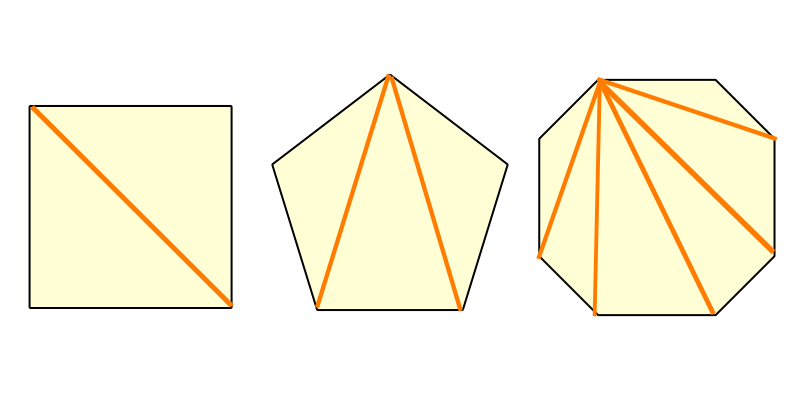
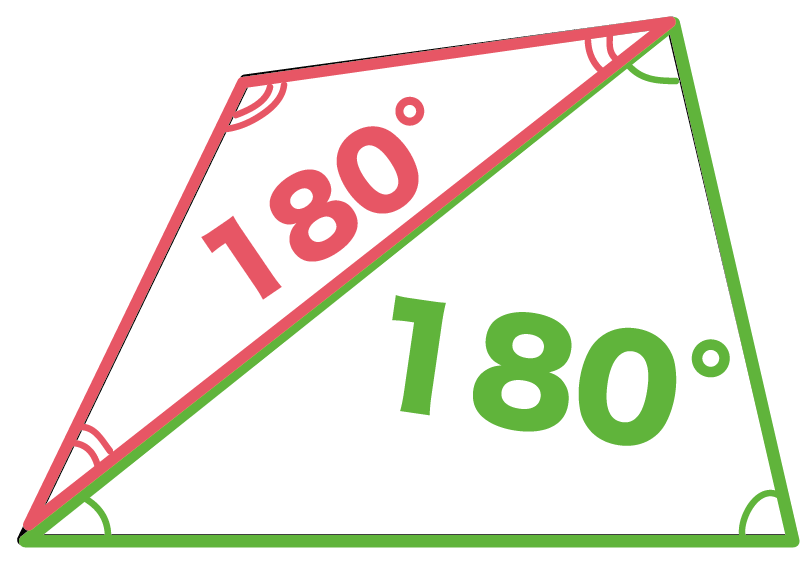
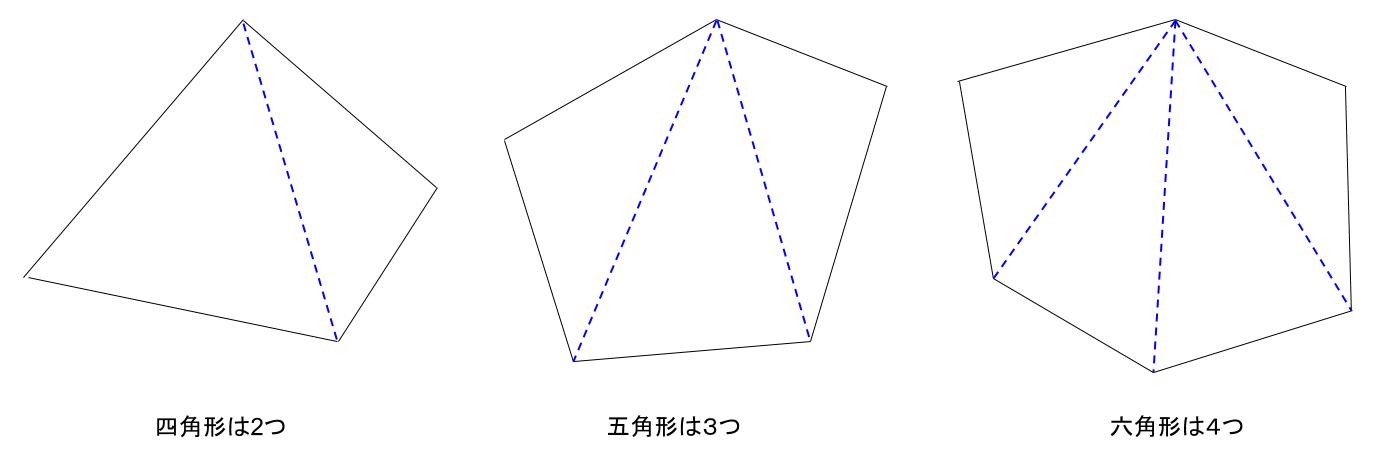
外角は図2のような角では ない 各内角には2つの外角があるが,外角の大きさというときにはそのうちの 1つ だけを指す 多角形の外角の和は 360° である 外角を辺に沿って集めると,1点の周りの角になる 1点のまわりの角は 360° であるから,外角の和は 360° に四角形の内角の和のポイント ・ 四角形は、2つの三角形に分けることができます。 ・ 四角形の内角の和は、三角形2つ分の内角の和なので、180°×2=360°となります。四角形は三角形が2つ 五角形は三角形が3つ 六角形は三角形が4つ ・・・ と増えていくだけです。 なので多角形の内角の和は三角形の数に関係しています。 三角形の内角の和は\(\,180°\,\) これは忘れたら角度は求まりません。 多角形の内角の和の公式を表し
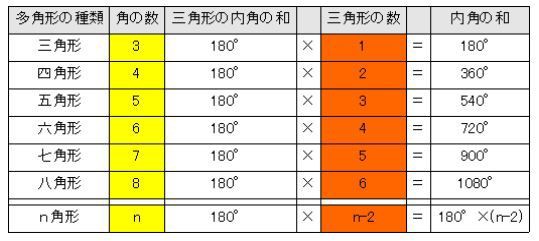
対角の和が180°である四角形は、円に内接する。 「円に内接する四角形の対角の和は180°である」 円に内接する四角形 数式で独楽する の逆の命題です。図を用いると、 四角形abcdについて∠a ∠c = 180°ならば、四角形abcdは円に内接する。 ということです。3点a, b, dを通る円を描11角形 16° 12角形 1800° 5角形までの内角の和は覚えましょう。 多角形の内角の和は下の公式で求められます。 角形の内角の和 = 180 × ( 2) 例えば8角形の内角の和は 180 × (8 2) = 1080四角形の内角の和は、 180 × (4 − 2) = 360 ∘ 五角形の内角の和は、 180 × (5 − 2) = 540 ∘ 六角形の内角の和は、 180 × (6 − 2) = 7 ∘




課題学習の指導 数学




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト
2-4-1 星型多角形の内角の和 教材(問題場面) ※m 点とばし星型n 角形の内角の和は180°×(n-2-2m)と表すことができる。 180° 360° 540° 7° 900° 1080° 1260° 1440° 180° 180° 180° 360° 360° 360° 540° 540° 7°多角形(四角形・五角形・六角形・・・)の内角の和の公式 多角形の内角の和の公式と外角の和を利用した角度の求め方 中2数学正多角形の外角の大きさが3秒でわかる公式 多角形の内角の和・外角の和は?正多角形の内角の求め方は 多角形の内角の和の公式 三角形の内角の和: 180° 180 ° 四角形の内角の和: 360° 360 ° 五角形の内角の和: 540° 540 °



3




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学
(四角形の内角の和) = 360° ここまでは大抵の人が知っていると思いますが、六角形や八角形などを覚えている人は少ないかもしれません。 そこで今日は 簡単に覚えられる多角形の内角の和を紹介していこうと思います。多角形の内角の和と外角の和の公式をまとめると以下の通り。 N角形の内角の和:180°× (N −2) 180 ° × ( N − 2 ) 多角形の外角の和:360° 360 ° 内角の和は三角形の180°から、角が増えるごとに180°ずつ増えていきます。 それに対し、外角の和は角が 外角・内角の和、面積、対角線の本数の公式と求め方 21年2月19日 この記事では、「多角形」の種々の公式(外角の和・内角の和、面積、対角線の本数など)やその求め方をわかりやすく解説していきます。 また計算問題の解き方もわかりやすく解説して



動画 多角形の内角の和 Youtube



Q Tbn And9gctqxnxegjdxp Adpruavnpmf2sansioyhqkmwlqdbcw Fiiw67x Usqp Cau
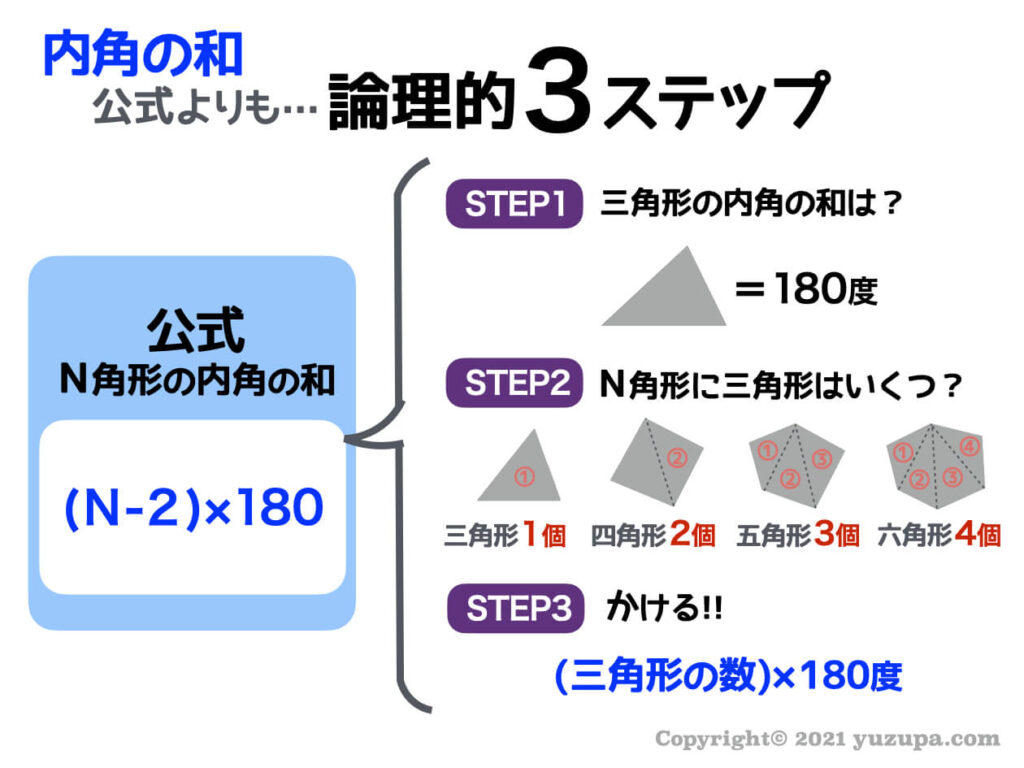
・この公式を理解するためには、三角形の内角の和は180°という公式を使います。 このn角形の内角の和の公式は、中学生で習う内容です。 ただ、実は 小学生でも多角形の内角の和について習っている ので、その復習にもなっている公式です。N角形の内角の和は180 (n2)なので n=10を代入すると 180 (102)=180×8=1440° 正八角形の1つの外角 多角形の外角の和はどれも360°なので 360°÷8=45° 確認 ① 十二角形の内角の和を求めよ。 ② 正九角形の一つの外角は何度か。 答①1800° ②40°四角形 四角形の概要 Weblio辞書;
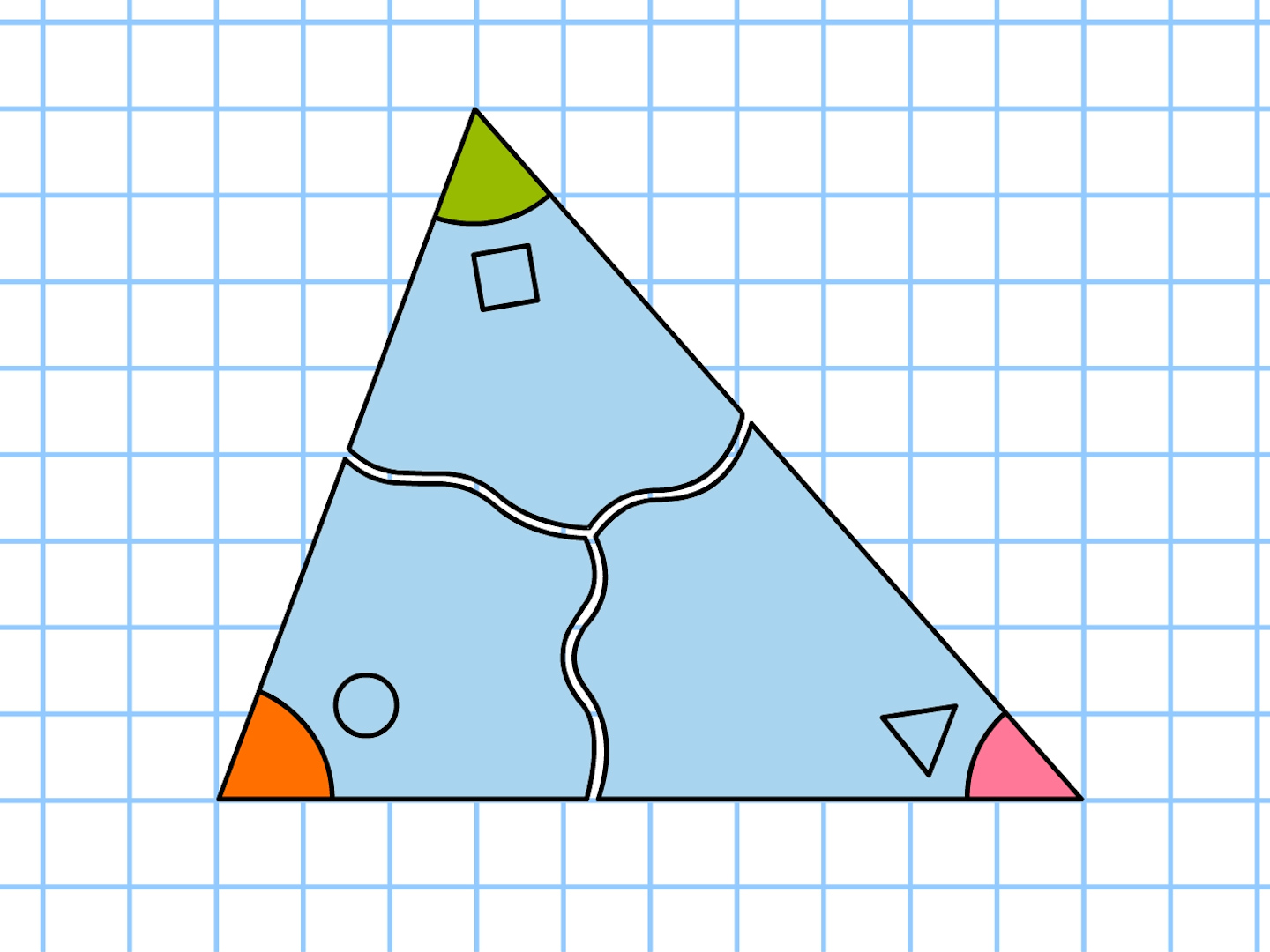



5年 三角形のふしぎ 算数イメージ動画集 大日本図書




四角形の内角の和を求める問題で 四角形に 三角形を上に足して求める方法が理解 Clear
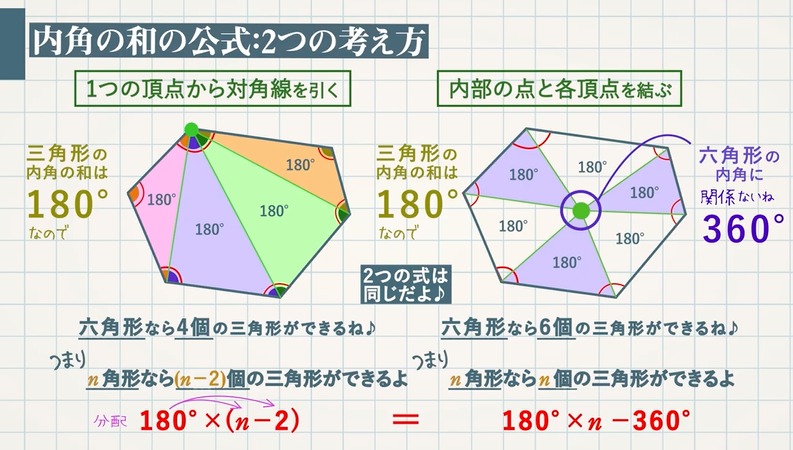
内角の和の公式を導く $2$ つの考え方を確認しましょう。 ① $\textcolor{green}{1}$ つの頂点から対角線を引く 対角線を引くと、六角形なら $4$ 個$(62 個)$の三角形ができます。無料ダウンロード・印刷できる、四角形・多角形の角度を求める問題プリントです。 四角形や多角形の内角の和の決まりを利用して特定の角の大きさを求める練習をします。 小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント 円に内接する四角形の性質まとめ対角の和が180°になる理由 Tooda Yuuto 18年8月22日 / 19年9月9日 四角形の つの頂点 がすべて同じ円周上にある(内側から接している)とき、「四角形 は円に内接する」といいます。 反対に、四角形 の つの辺がすべて
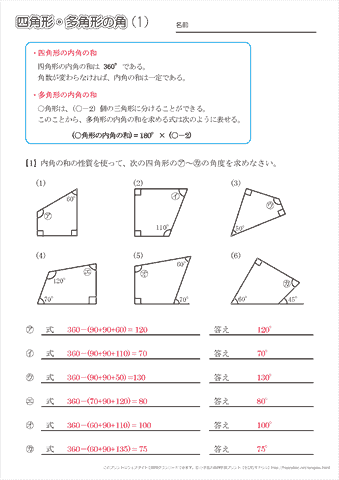



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生



多角形の内角と外角 思考力を鍛える数学
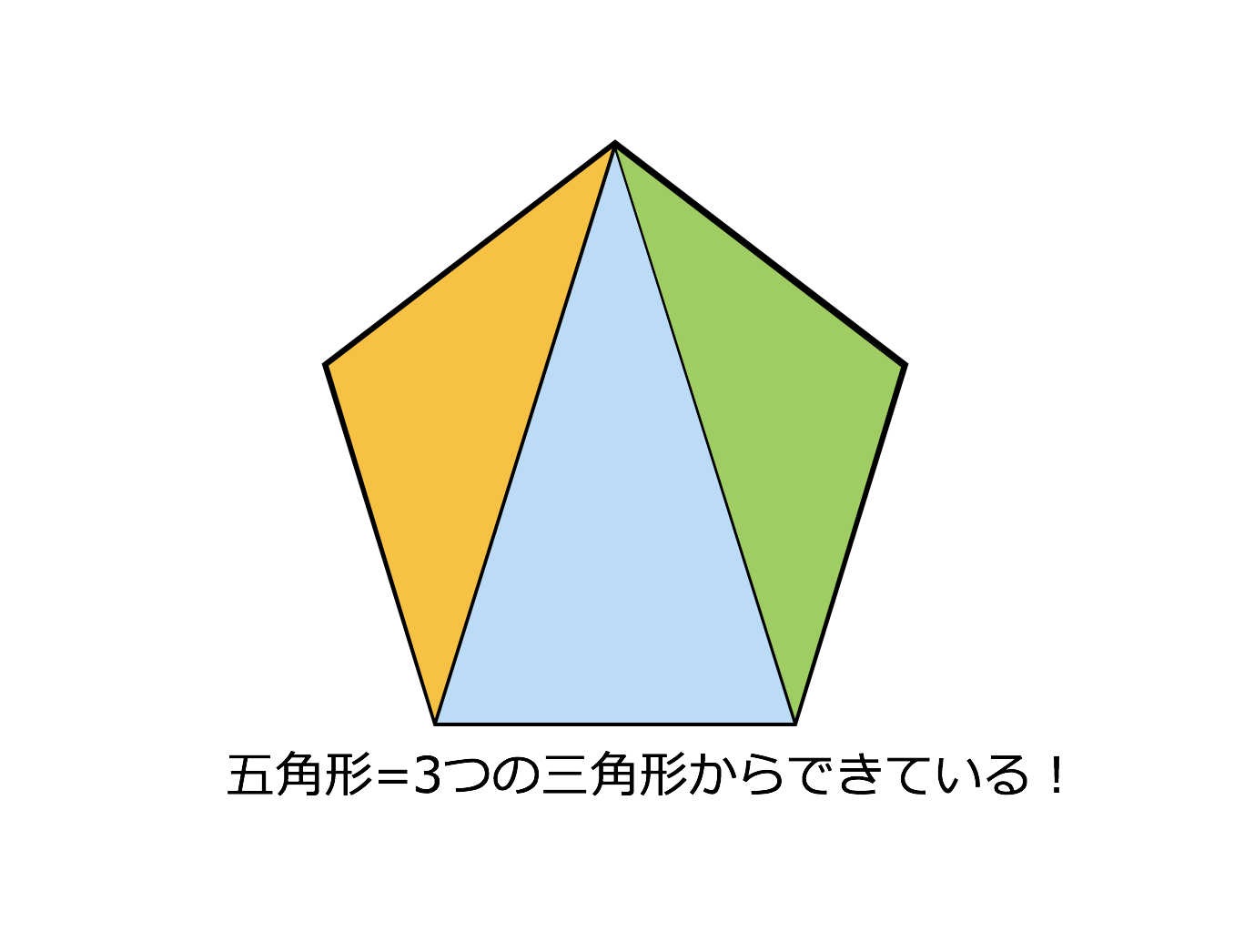
多角形の内角の和と外角の和の公式 n角形の内角の和:180°×(n−2)180°×(n−2) 多角形の外角の和:360°360° 難しく感じるかもしれませんが、内角の和は三角形が180°。 そこから角が増えるごとに内角の和も180°ずつ増えていきますよーということです。 多角形の内角の和を求める公式 多角形の内角の総和は、上記のように補助線を引いて三角形がいくつできるかで知ることができます。 また、上記のことから、以下の公式を導くことができます。 多角形の内角の和 = 180° × ( 頂点の数 - 2 )内角の和と三角形の関係は?1分でわかる和の値、証明、外角との関係 多角形の内角の和は?1分でわかる公式、問題の求め方、簡単な証明 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも読める!広告無し!




無料 中2数学 基本解説 解答プリント 223 図形3 多角形の角



1
上の事実は次のように説明できます. まず, 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので, n n 角形の内角と外角の和の合計は, 180°×n 180 ° × n です.そして, n n 角形の外角の和は,これから内角の和をひいたものなので, 180多角形(四角形・五角形・六角形・・・)の内角の和の公式 正方形 正三角形 正六角形; 四角形の内角の和を「帰納的に」360度であると求めた後、どのように授業を展開しますか? 教科書では、 「 すべての四角形について、360度であると調べたわけではない(帰納的) から、 どんな四角形についても360度であることを調べる方法(演繹的) は



南山中学女子部過去問題演習
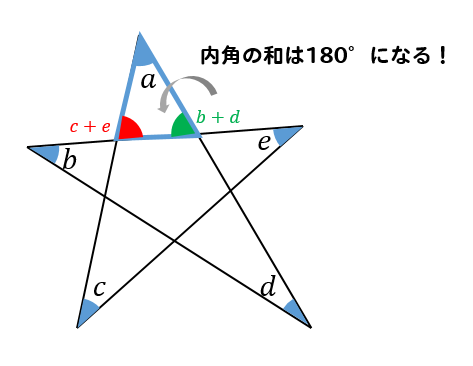



星形の角度 内角の和の求め方を問題解説 数スタ
四角形に関する用語 対辺:繋がっていない(頂点を共有しない)辺のこと。四角形は2組の対辺を持つ(向かい合う辺)。 対頂点:辺を共有しない二頂点。四角形は2組の対頂点を持つ。 対角:対頂点における内角。 四角形は2組の対角を持つ(向かい合う角)。 正多角形の内角を4秒で計算できる公式 正多角形の内角を計算したいんだけど?? こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。 正多角形の内角 を知りたいときってあるよね?? 多角形の内角の和は公式つかえばドヤ顔できるけど、三角形の内角の和を 基にして,四角形の 内角の和の求め方を 演繹的に考え,説明 することができる。 本授業アイディア例との関連 小学校:数学的な考え方の評価規準 中学校:数学的な見方や考え方の評価規準 図形の角 三角形の内角の和を基




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
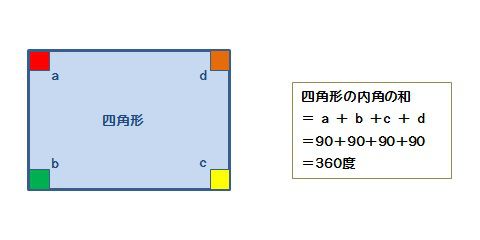
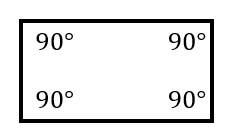
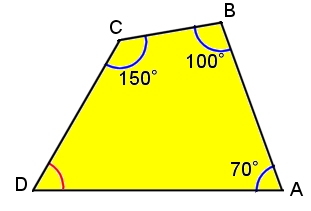
下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 °四角形の内角の和を考えるときは 長方形や正方形で考えるのが簡単だと思います。 長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度面積計算機 六角形 公式 対辺 求め方 6角形;
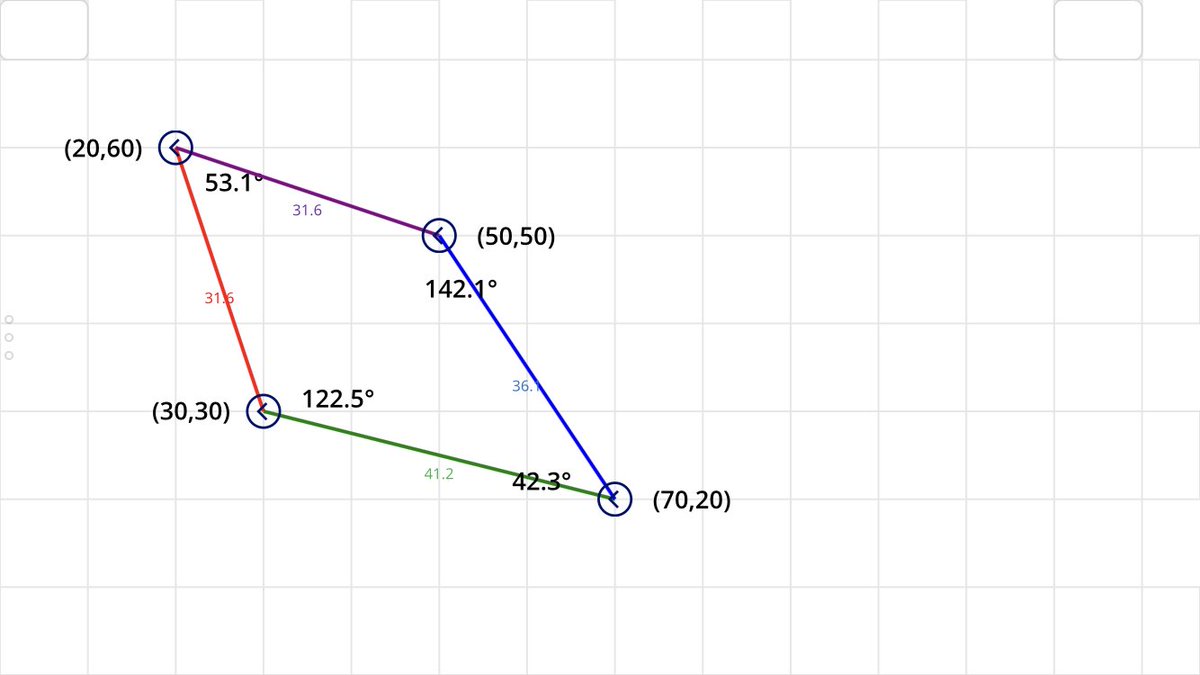



Hiro 四角形の内角の和は常に360です とか 平行四辺形は向かい合う角の角度が一緒で隣り合う角の和は180です みたいな教育に最適じゃないか いいもの作った 自画自賛




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
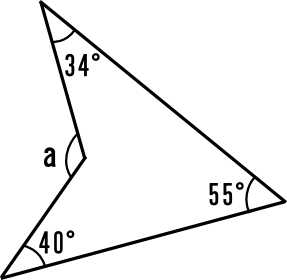
を証明できました。ここで,任意の三角形に対して面積 S > 0 S > 0 S > 0 なので A B C > π ABC > \pi A B C > π が成立します! つまり, 球面上の三角形の内角の和は π \pi π より大きい ことがわかります。 三角形の面積を考えることで内角の和が評価できる 四角形の内角の和は、 360° だったよね?? この「360°」から2つの角度をひけばいいんだ。 平行四辺形abcdでいうと、 「角a」と 「角c」が1°ってことがわかった。 つまり、こいつらを足すと、 240°になるはずだ。 これを四角形の内角の和360°からひいてすべての内角が $180^\circ$ 未満である四角形 $\mathrm{ABCD}$ が直径 $1$ の円に内接している 弧 $\mathrm{AB},$ $\mathrm{BC},$ $\mathrm{CD




内角の和 算数用語集




中2数学 複雑な多角形 角の和 応用問題
三角形の内角の和は180度 , 四角形の内角の和は360度です。 では五角形 , 六角形 の内角の和はいくつになるのでしょうか。 角形の内角の和の公式=180× ( -2) ※ 絶対に覚えておいて下さい。 例えば 五角形の内角の和=180× (5-2)=180×3=540度 六角形三角形の内角の和は 180 ∘ でしたが、 四角形の内角の和は必ず 360 ∘ になります。 例えば、長方形や正方形は、全ての角度が 90 ∘ であり、全て足すと 90 90 90 90 = 360 ∘




四角形の内角の和 授業のポイント 算数を究める



凹四角形の外角の和についての質問です 内角が60 40 3 Yahoo 知恵袋



Http Www Pref Kochi Lg Jp Soshiki Files File 1 Pdf



Just For Today
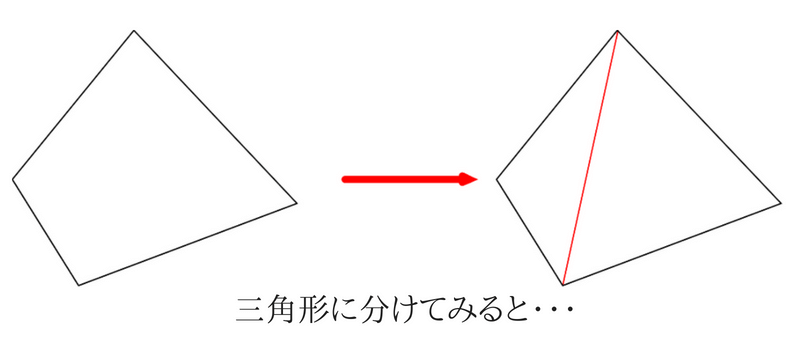



三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
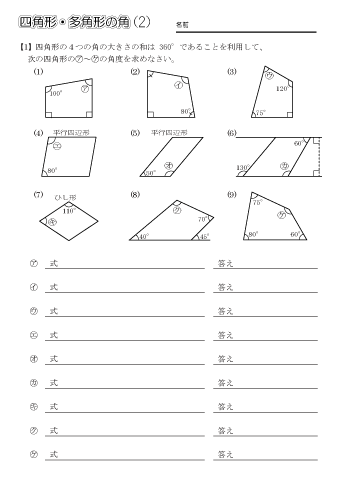



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




内角の和 180 N 2 外角の和 360 教遊者




三角形の内角の和を帰納的 演繹的に求める方法 算数を究める



ラングレーの問題 整角四角形




n角形の内角の和 中2 多角形の内角と外角 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles




内角の和 180 N 2 外角の和 360 教遊者
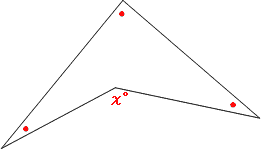



角度の求め方 算数の教え上手 学びの場 Com




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の内角の和 は何度なのか を説明します おかわりドリル




小学校5年 算数 四角形の内角の和 Youtube



1




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形の性質 第4回 外角の和について なぜ360 になるのか 算数パラダイス




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト




内角の和 180 N 2 外角の和 360 教遊者




中学2年生の数学 内角の和 外角の和の復習 塾講師が数学をやりmath




多角形の内角の和 は何度なのか を説明します おかわりドリル
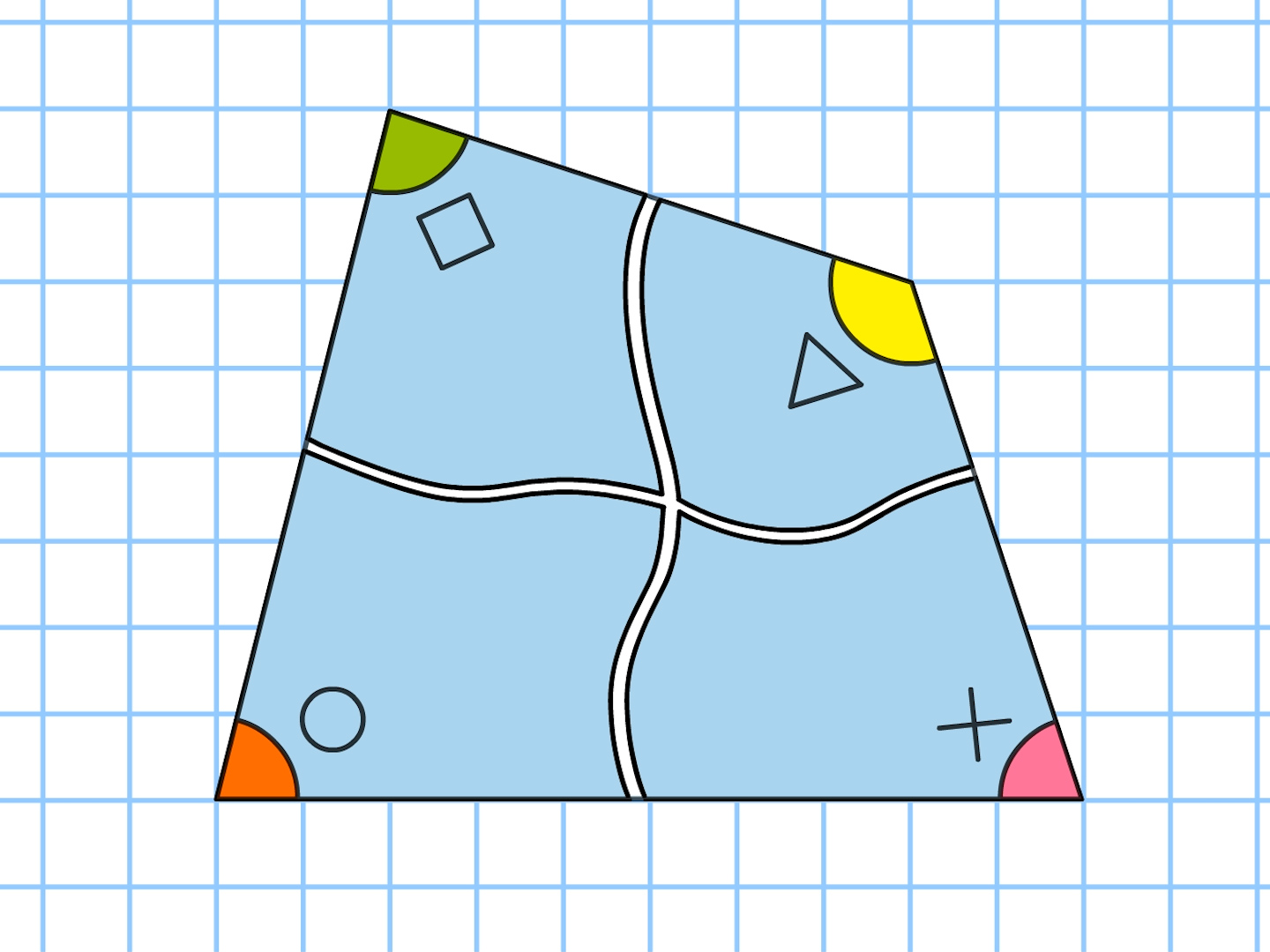



5年 四角形のふしぎ 算数イメージ動画集 大日本図書



Www Saga Ed Jp Kenkyu Kenkyu Chousa H23 03 sho Sansuu H21shou San Jyugyou Documents Kaku03 Pdf




小学校5年 算数 四角形の内角の和 Youtube




内角と外角の性質 下の三角形の載っている問題なのですが 解説の意味が分か Okwave
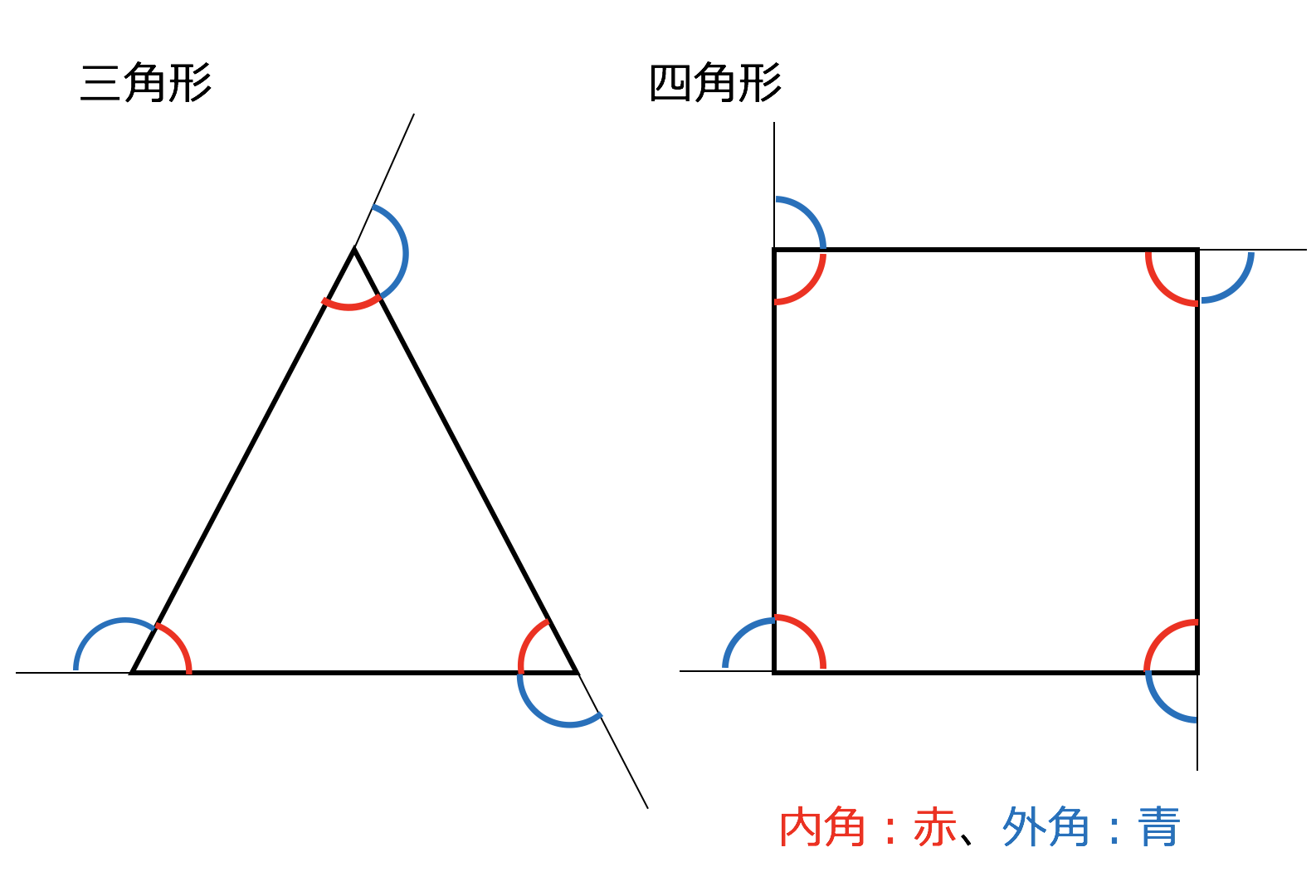



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
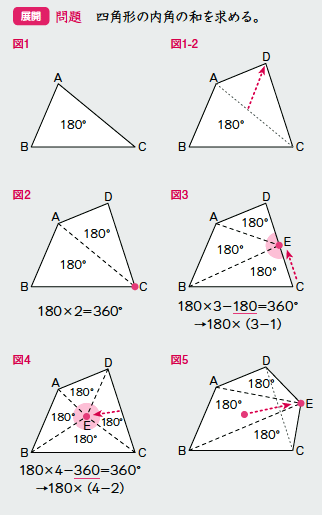



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所




つくばサイエンスエッジ18 文京学院大学女子高校 みらいぶ 高校生サイト




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題
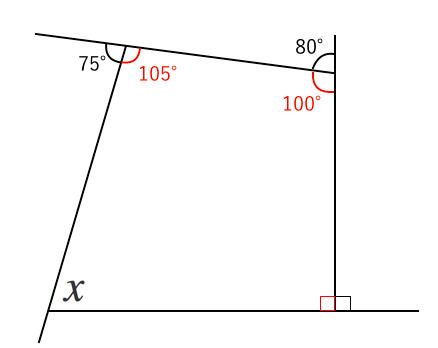



図形の調べ方 外角を求める 苦手な数学を簡単に



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
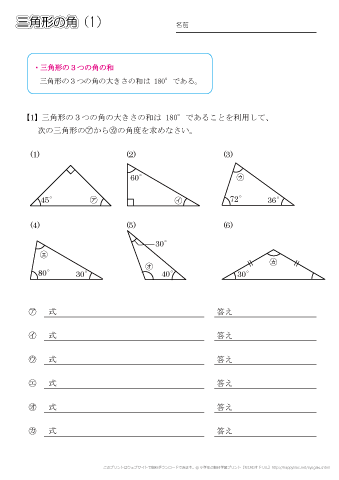



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




朝日新聞デジタル 内角の和 わくわく360度 花まる先生公開授業 教育
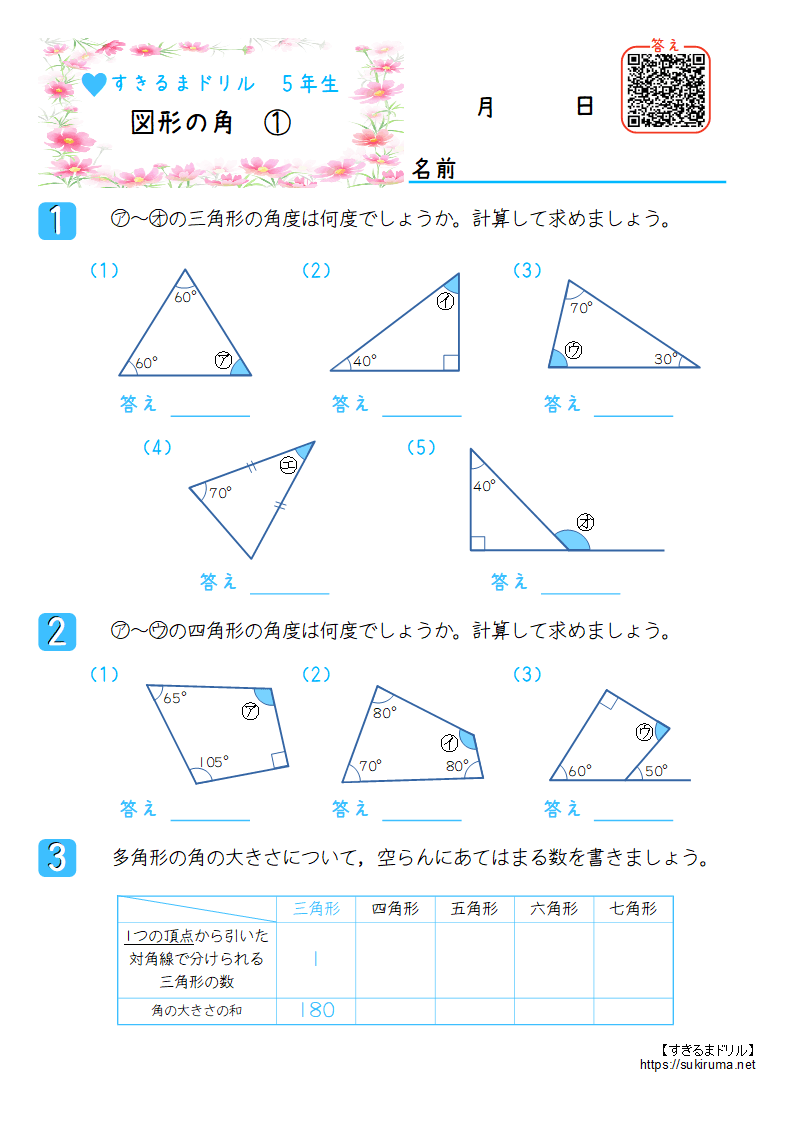



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント




四角形の内角の和 スクールプレゼンター教材共有サイト スクプレ道場




多角形の内角の和 外角の和の公式 数学fun




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題
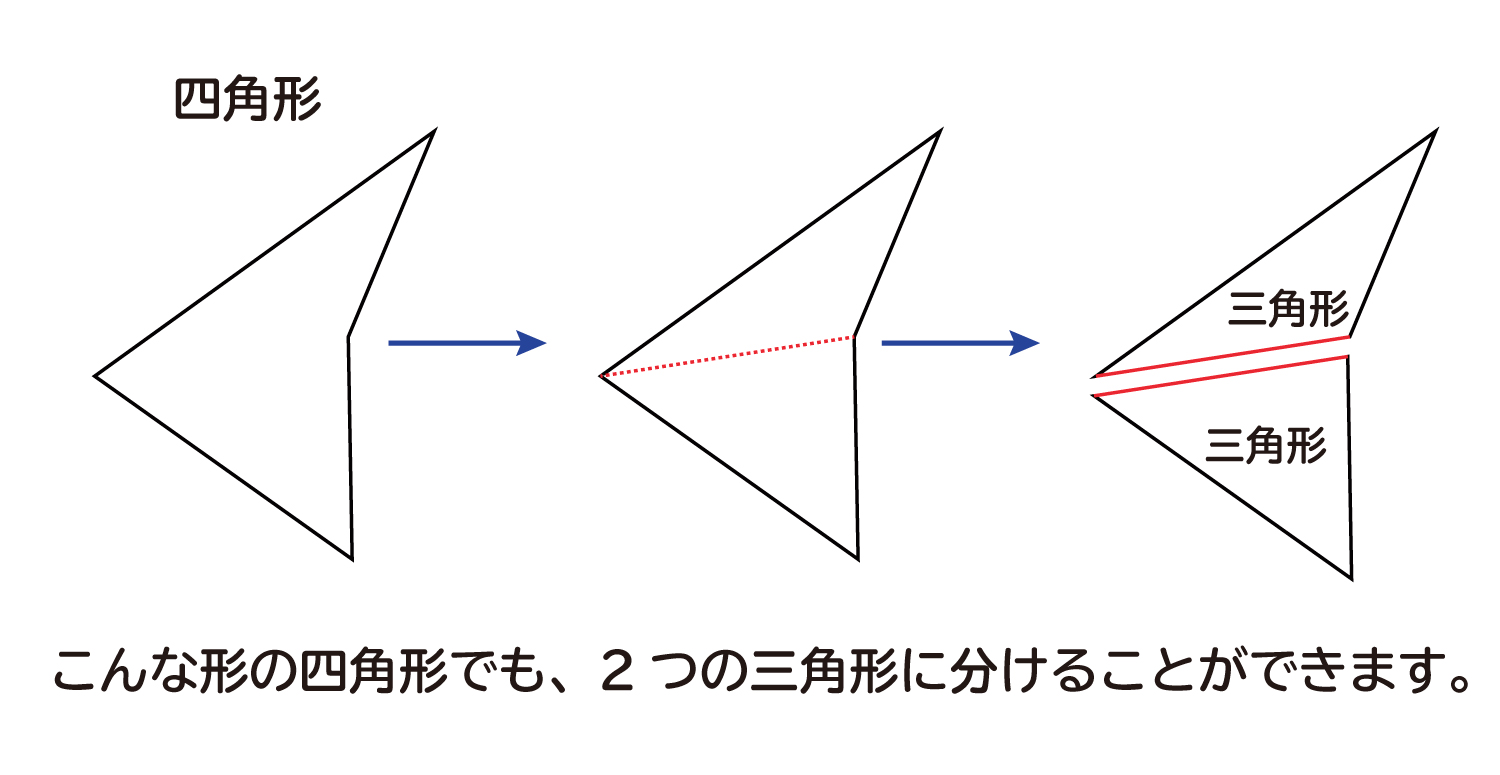



多角形の内角の和 は何度なのか を説明します おかわりドリル



Http Www Asahikawa Hkd Ed Jp Nagayama Jhs 221 Ef 92 E5 B9 B4 E6 95 B0 E5 Ad A6 Ef E5 9b E5 80 80 E5 9a E8 92 E5 81 Ae E5 86 85 E8 92 81 A8 E5 96 E8 92 80 80 E8 A3 E7 Ad 94 Ef Pdf
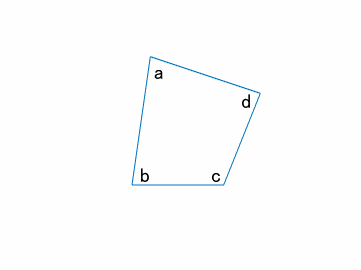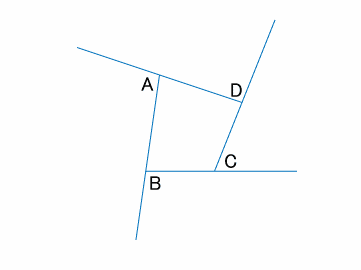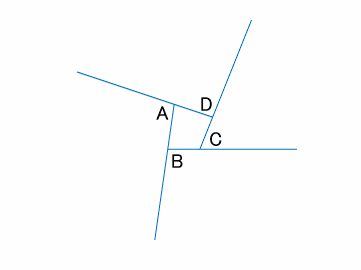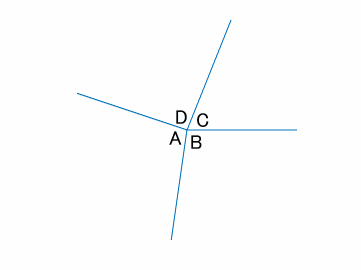



なぜ三角形の内角の和は180度 Qiita




数学 中2 51 多角形の内角と外角の和 基本編 Youtube
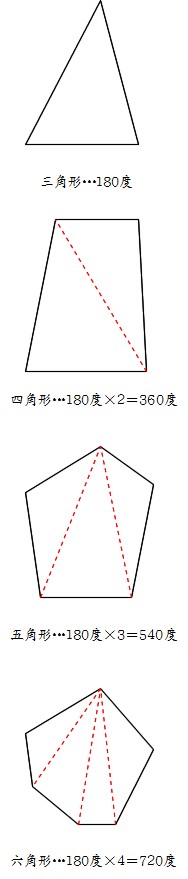



Math 多角形の内角の和 働きアリ
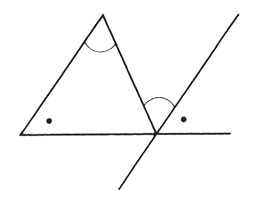



内角の和 算数用語集



多角形の内角と外角 思考力を鍛える数学



12個の角の和を求められますか 油断大敵を地で行く問題 秒刊sunday



四角形の内角の和 算数の公式覚えてますか




多角形の内角の和 算数の公式覚えてますか



内角攻め それとも外角攻め すうがくラボのブログ
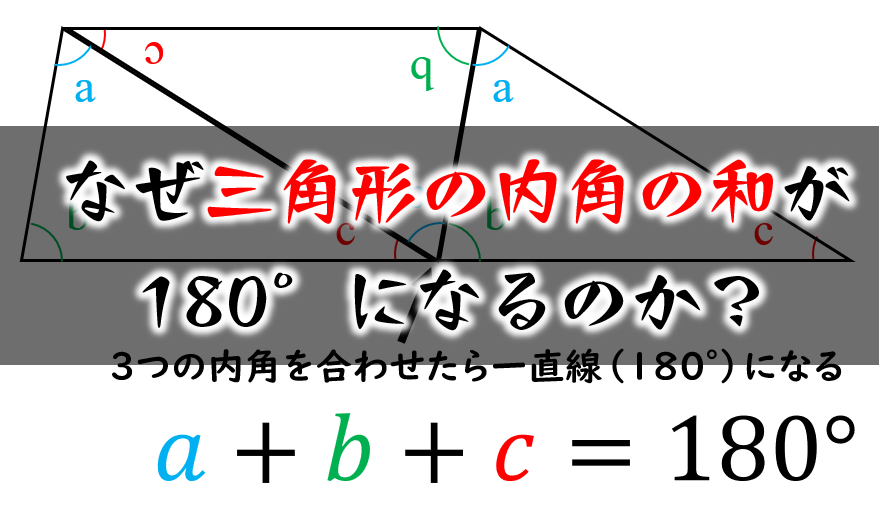



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
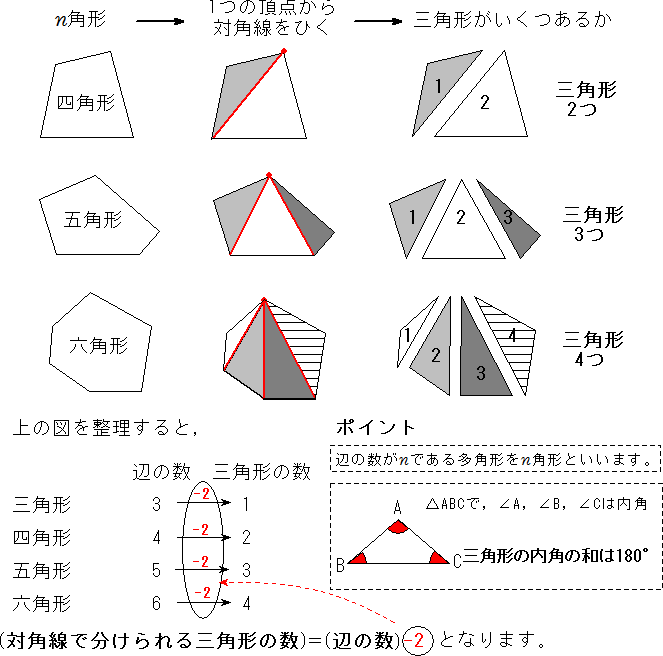



三角形と四角形 多角形の内角の和 中学数学 定期テスト対策サイト
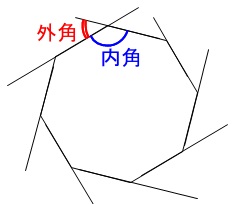



多角形の内角の和の公式と外角の和を利用した角度の求め方
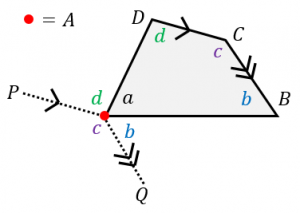



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学




四角形の内角の和 On Vimeo




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学



多角形の内角の和 簡単に計算できる電卓サイト




多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



中学2年数学練習問題 図形の調べ方 多角形の内角と外角
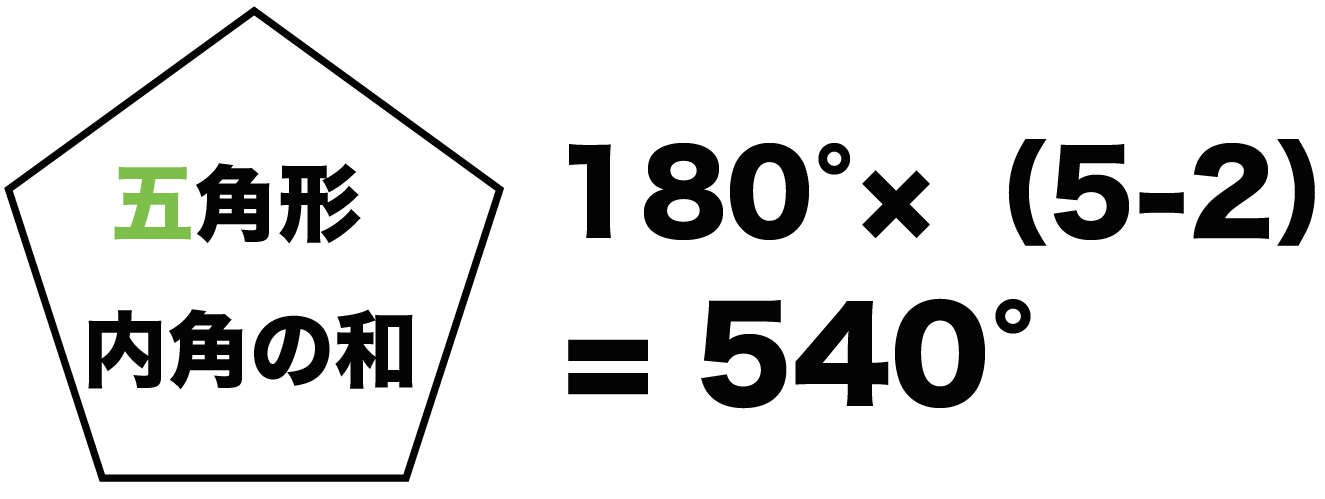



中2数学 多角形の内角の和が3秒でわかる公式 Qikeru 学びを楽しくわかりやすく



四日市市立日永小学校




中2 中2 数学 内角の和 授業ノート 中学生 数学のノート Clear
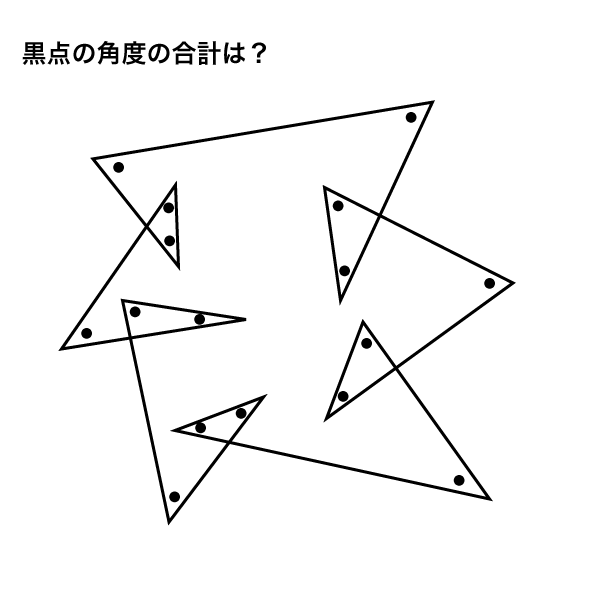



角度情報がない図形の合計の角度 星形多角形 受験算数入門
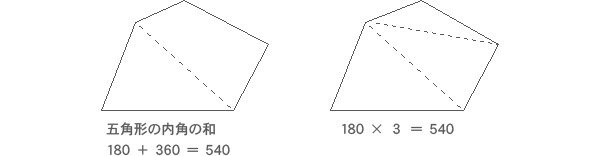



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版
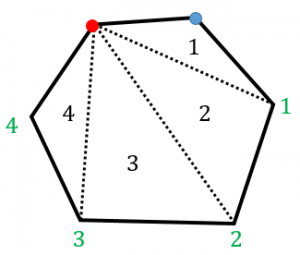



多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



多角形の内角の和は 1分でわかる公式 問題の求め方 簡単な証明



Http Www Sendai C Ed Jp 02kensyu 02cyoken H27 Yoshida S Pdf
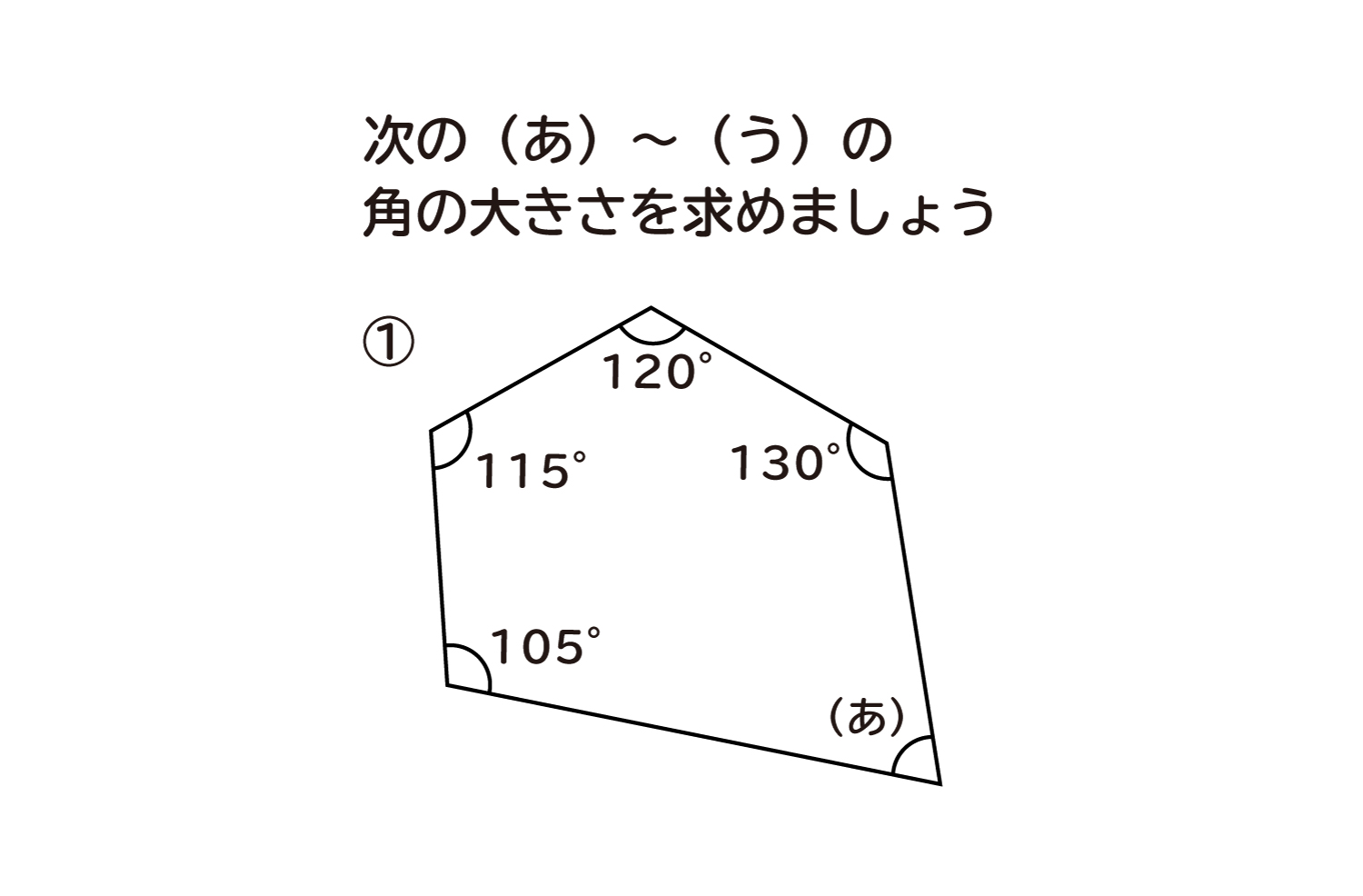



小学5年生 算数 無料問題集 多角形の角の大きさ おかわりドリル



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



内角の和 180 N 2 外角の和 360 教遊者



中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
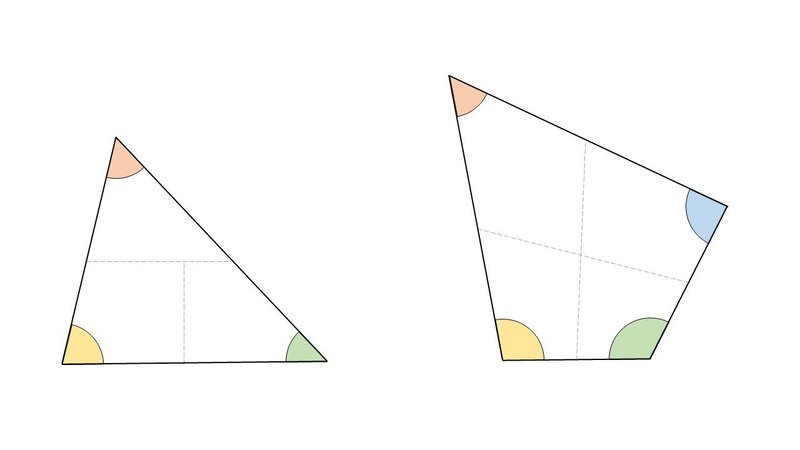



算数工作 三角形と四角形の内角の和を調べてみよう 外角の和のデータも公開中 Math Channel Note



いろいろな問題




中2数学 複雑な多角形 角の和 応用問題



中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
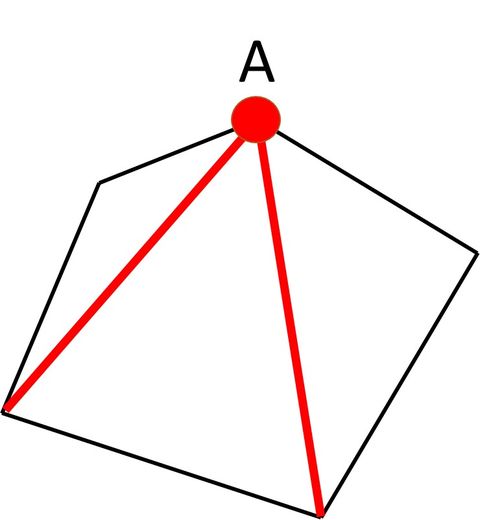



多角形の内角の和はなぜ n 2 のぶちゃん先生の花まる教室



0 件のコメント:
コメントを投稿